题目内容
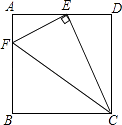
【题目】如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF= . 
【答案】![]()
【解析】解:∵四边形ABCD是正方形, ∴AD=DC,∠A=∠D=90°,
∵AE=ED,
∴CD=AD=2AE,
∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠DEC+∠DCE=90°,
∴∠AEF=∠DCE,∵∠A=∠D,
∴△AEF∽△DCE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴tan∠ECF= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】通过灵活运用正方形的性质和锐角三角函数的定义,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中C组所在的扇形的圆心角为36° 被抽取的体育测试成绩频数分布表
组别 | 成绩 | 频数 |
A | 20<x≤24 | 2 |
B | 24<x≤28 | 3 |
C | 28<x≤32 | 5 |
D | 32<x≤36 | b |
E | 36<x≤40 | 20 |
合计 | a | |
根据上面的图表提供的信息,回答下列问题: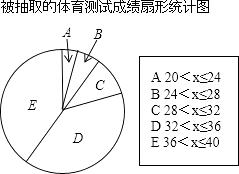
(1)计算频数分布表中a与b的值;
(2)根据C组28<x≤32的组中值30,估计C组中所有数据的和为;
(3)请估计该校九年级学生这次体育测试成绩的平均分(结果取整数).
【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
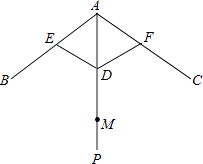
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.