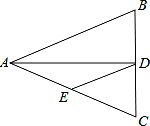
题目内容
在 中,
中,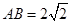 ,
, ,
,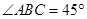 ,以AB为一边作等腰直角三角形ABD,使
,以AB为一边作等腰直角三角形ABD,使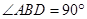 ,连结CD,则线段CD的长为__________.
,连结CD,则线段CD的长为__________.
 中,
中,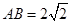 ,
, ,
,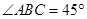 ,以AB为一边作等腰直角三角形ABD,使
,以AB为一边作等腰直角三角形ABD,使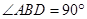 ,连结CD,则线段CD的长为__________.
,连结CD,则线段CD的长为__________.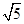 或
或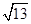 .
.试题分析:分两种位置关系进行讨论:
①点A、D在BC的两侧,设AD与边BC相交于点E,根据等腰直角三角形的性质求出AD,再求出BE=DE=
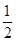 AD 并得到BE⊥AD,然后求出CE,在Rt△CDE中,利用勾股定理列式计算即可得解;
AD 并得到BE⊥AD,然后求出CE,在Rt△CDE中,利用勾股定理列式计算即可得解;②点A、D在BC的同侧,根据等腰直角三角形的性质可得BD=AB, 过点D作DE⊥BC交BC的反向延长线于E,判定△BDE是等腰直角三角形,然后求出DE=BE=2,再求出CE,然后在Rt△CDE中,利用勾股定理列式计算即可得解.
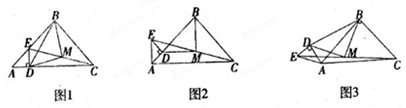
试题解析:①如图1,点A、D在BC的两侧,
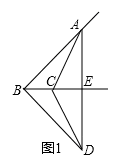
∵△ABD是等腰直角三角形,
∴AD=
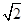 AB=
AB=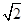 ×2
×2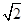 =4,
=4,∵∠ABC=45°,
∴BE=DE=
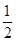 AD=
AD=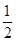 ×4=2,BE⊥AD,
×4=2,BE⊥AD,∵BC=1,
∴CE=BE-BC=2-1=1,
在Rt△CDE中,CD=
 ;
;②如图2,点A、D在BC的同侧,
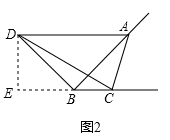
∵△ABD是等腰直角三角形,
∴BD=AB=2
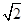 ,
,过点D作DE⊥BC交BC的反向延长线于E,则△BDE是等腰直角三角形,
∴DE=BE=
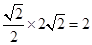 ,
,∵BC=1,
∴CE=BE+BC=2+1=3,
在Rt△CDE中,CD=
 ,
,综上所述,线段CD的长为
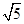 或
或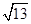 .
.考点: 1.勾股定理;2.等腰直角三角形.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目