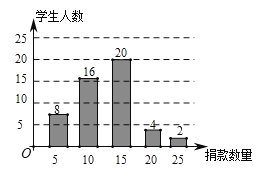
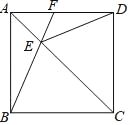
题目内容
【题目】已知△ABC内接于⊙O,AD平分∠BAC.
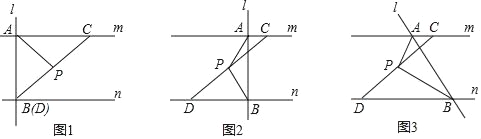
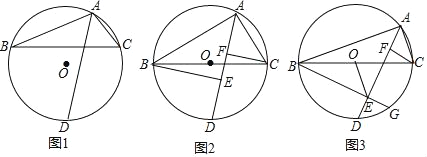
(1)如图1,求证:![]() ;
;
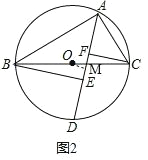
(2)如图2,当BC为直径时,作BE⊥AD于点E,CF⊥AD于点F,求证:DE=AF;
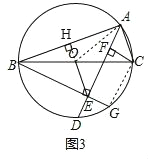
(3)如图3,在(2)的条件下,延长BE交⊙O于点G,连接OE,若EF=2EG,AC=2,求OE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)2.
【解析】
(1)连接OB、OC、OD,根据圆心角与圆周角的性质得∠BOD=2∠BAD,∠COD=2∠CAD,又AD平分∠BAC,得∠BOD=∠COD,再根据圆周角相等所对的弧相等得出结论.
(2)过点O作OM⊥AD于点M,又一组角相等,再根据平行线的性质得出对应边成比例,进而得出结论;
(3)延长EO交AB于点H,连接CG,连接OA,BC为⊙O直径,则∠G=∠CFE=∠FEG=90°,四边形CFEG是矩形,得EG=CF,又AD平分∠BAC,再根据邻补角与余角的性质可得∠BAF=∠ABE,∠ACF=∠CAF,AE=BE,AF=CF,再根据直角三角形的三角函数计算出边的长,根据“角角边”证明出△HBO∽△ABC,根据相似三角形的性质得出对应边成比例,进而得出结论.
(1)如图1,连接OB、OC、OD,
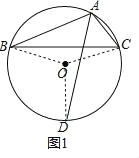
∵∠BAD和∠BOD是![]() 所对的圆周角和圆心角,
所对的圆周角和圆心角,
∠CAD和∠COD是![]() 所对的圆周角和圆心角,
所对的圆周角和圆心角,
∴∠BOD=2∠BAD,∠COD=2∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠BOD=∠COD,
∴![]() =
=![]() ;
;
(2)如图2,过点O作OM⊥AD于点M,
∴∠OMA=90°,AM=DM,
∵BE⊥AD于点E,CF⊥AD于点F,
∴∠CFM=90°,∠MEB=90°,
∴∠OMA=∠MEB,∠CFM=∠OMA,
∴OM∥BE,OM∥CF,
∴BE∥OM∥CF,
∴![]() =
=![]() ,
,
∵OB=OC,
∴![]() =
=![]() =1,
=1,
∴FM=EM,
∴AM﹣FM=DM﹣EM,
∴DE=AF;
(3)延长EO交AB于点H,连接CG,连接OA.
∵BC为⊙O直径,
∴∠BAC=90°,∠G=90°,
∴∠G=∠CFE=∠FEG=90°,
∴四边形CFEG是矩形,
∴EG=CF,
∵AD平分∠BAC,
∴∠BAF=∠CAF=![]() ×90°=45°,
×90°=45°,
∴∠ABE=180°﹣∠BAF﹣∠AEB=45°,
∠ACF=180°﹣∠CAF﹣∠AFC=45°,
∴∠BAF=∠ABE,∠ACF=∠CAF,
∴AE=BE,AF=CF,
在Rt△ACF中,∠AFC=90°,
∴sin∠CAF=![]() ,即sin45°=
,即sin45°=![]() ,
,
∴CF=2×![]() =
=![]() ,
,
∴EG=![]() ,
,
∴EF=2EG=2![]() ,
,
∴AE=3![]() ,
,
在Rt△AEB中,∠AEB=90°,
∴AB=![]() =
=![]() =6,
=6,
∵AE=BE,OA=OB,
∴EH垂直平分AB,
∴BH=EH=3,
∵∠OHB=∠BAC,∠ABC=∠ABC
∴△HBO∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴OH=1,
∴OE=EH﹣OH=3﹣1=2.