题目内容
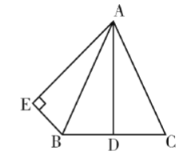
【题目】如图,在正方形ABCD中,E为对角线AC上一点,CE=CD,连接EB、ED,延长BE交AD于点F.求证:DF2=EFBF.
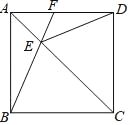
【答案】见解析
【解析】
证明△FDE∽△FBD即可解决问题.
∵四边形ABCD是正方形,
∴BC=CD,且∠BCE=∠DCE,
又∵CE是公共边,
∴△BEC≌△DEC,
∴∠BEC=∠DEC.
∵CE=CD,
∴∠DEC=∠EDC.
∵∠BEC=∠DEC,∠BEC=∠AEF,
∴∠EDC=∠AEF.
∵∠AEF+∠FED=∠EDC+∠ECD,
∴∠FED=∠ECD.
∵四边形ABCD是正方形,
∴∠ECD=![]() ∠BCD=45°,∠ADB=
∠BCD=45°,∠ADB=![]() ∠ADC=45°,
∠ADC=45°,
∴∠ECD=∠ADB.
∴∠FED=∠ADB.
又∵∠BFD是公共角,
∴△FDE∽△FBD,
∴![]() =
=![]() ,即DF2=EFBF.
,即DF2=EFBF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目