Question

【题目】在△ABC中，AB＝AC，AM是△ABC的外角∠CAE的平分线．

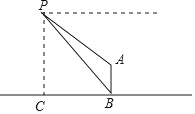
（1）如图1，求证：AM∥BC；

（2）如图2，若D是BC中点，DN平分∠ADC交AM于点N，DQ平分∠ADB交AM的反向延长线于Q，判断△QDN的形状并说明理由．

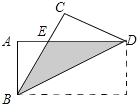
（3）如图3，在（2）的条件下，若∠BAC＝90°将∠QDN绕点D旋转一定角度，DN交边AC于F，DQ交边AB于H，当S△ABC＝14时，则四边形AHDF的面积为　 　．

Answer 1

【答案】（1）见解析；（2）△ADN是等腰直角三角形，理由见解析；（3）7.

【解析】

（1）先判断出∠B＝∠C，再用角平分线得出∠EAM＝∠MAC＝∠EAC，进而得出∠B＝∠EAC，即可得出结论；

（2）先判得出∠ADB＝∠ADC＝90°，进而借助角平分线判断出∠QDN＝90°，再判断出∠AND＝∠AQD，得出DQ＝DN，即可得出结论；

（3）先判断出△BDH≌△ADF，得出S△BDH＝S△ADF，进而得出S四边形AHDF＝S△ABD，即可得出结论．

解:（1）∵AB＝AC，

∴∠B＝∠C，

∵AM平分∠EAC，

∴∠EAM＝∠MAC＝∠EAC，

∵∠EAC＝∠B+∠C，

∴∠B＝∠EAC，

∴∠EAM＝∠B，

∴AM∥BC；

（2）△ADN是等腰直角三角形，理由：

∵D是BC的中点，AB＝AC，

∴AD⊥BC，

∴∠ADB＝∠ADC＝90°，

∵DN平分∠ADC，DQ平分∠ADB，

∴∠ADN＝∠NDC＝45°，∠ADQ＝∠BDQ＝45°，

∴∠QDN＝90°，

∵AM∥BC，

∴∠AND＝∠NDC＝45°，∠AQD＝∠BQD＝45°，

∴∠AND＝∠AQD，

∴DQ＝DN，

∴△ADN是等腰直角三角形；

（3）由（2）知，∠QDN＝90°，

∵∠BAC＝90°，

∴∠QDN+∠BAC＝180°，

∴∠AHD+∠AFD＝180°，

∵∠AHD+∠BHD＝180°，

∴∠BHD＝∠AFD，

由（2）知，∠ADB＝∠QDN＝90°，

∴∠BDH＝∠ADF，

在Rt△ABC中，AB＝AC，∠ADC＝90°，

∴BD＝CD＝AD，

∴△BDH≌△ADF（AAS），

∴S△BDH＝S△ADF，

∴S四边形AHDF＝S△ADF+S△ADH＝S△BDH+S△ADH＝S△ABD＝S△ABC＝7，

故答案为：7．