题目内容
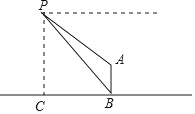
【题目】如图,一个热气球悬停在空中,从热气球上的P点测得直立于地面的旗杆AB的顶端A与底端B的俯角分别为34°和45°,此时P点距地面高度PC为75米,求旗杆AB的高度(结果精确到0.1米).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67)
【答案】24.8米.
【解析】
过点A作AH⊥PC于点H,则四边形ABCH是矩形,分别解直角三角形,求出PC、PH的长度即可.
如图,过点A作AH⊥PC于点H,
依题意,∠PHA=∠PCB=90°,四边形ABCH是矩形,
∴AH=BC,AB=CH,
在Rt△PBC中,∠PCB=90°,∠PBC=45°,
∴∠BPC=45°,
∴PC=BC=75,
在RtPHA中,∠PHA=90°,∠PAH=34°,AH=BC=75,
tan∠PHA=![]() ,
,
∴PH=AHtan∠PAH=75×tan34°,
∴AB=HC=PC﹣PH=75﹣75×0.67=75×0.33=24.75≈24.8(米).

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目