题目内容
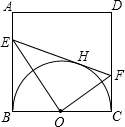
已知:如图,正方形ABCD的边长为2a,H是以BC为直径的半圆O上一点,过H与圆O相切的直线交AB于E,交CD于F。
(1)当点H在半圆上移动时,切线,EF在AB、CD上的两个交点也分别在AB、CD上移动(E、A不重合,F、D不重合),试问:四边形AEFD的周长是否也在变化?证观你的结论;
(2)设△BOE的面积为S1,△COF的面积为S2,正方形ABCD的面积为S,且S1+S2=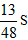 ,求BE与CF的长。
,求BE与CF的长。
(1)当点H在半圆上移动时,切线,EF在AB、CD上的两个交点也分别在AB、CD上移动(E、A不重合,F、D不重合),试问:四边形AEFD的周长是否也在变化?证观你的结论;
(2)设△BOE的面积为S1,△COF的面积为S2,正方形ABCD的面积为S,且S1+S2=
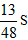 ,求BE与CF的长。
,求BE与CF的长。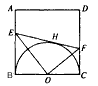
解:(1)由题意知,AB、CD、EF都与半圆相切,
∴EH=EB,FH=CF,
∴四边形AEFD的周长=AE+EH+HF+DF+AD=AE+EB+FC+DF+AD=6a,
∴四边形AEFD的周长是定值,没有变化;
(2)∵EO平分∠BEH,FO平分∠CFH,
∴OF⊥EO,
∵∠EOB、∠OFC同为∠FOC的余角,
∴∠EOB=∠OFC,
又∠EBO=∠OCF=90°,
∴△EBO∽△OCF,
∴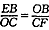 ,
,
即EB·CF=OC·OB=a2 ①
∵S1+S2=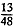 S,
S,
∴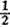 OB·BE+
OB·BE+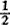 OC·CF=
OC·CF=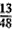 ·4a2,
·4a2,
即BE+CF=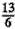 a…②
a…②
解①②得BE=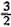 a,FC=
a,FC=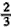 a;或BE=
a;或BE=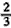 a,FC=
a,FC=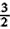 a。
a。
∴EH=EB,FH=CF,
∴四边形AEFD的周长=AE+EH+HF+DF+AD=AE+EB+FC+DF+AD=6a,
∴四边形AEFD的周长是定值,没有变化;
(2)∵EO平分∠BEH,FO平分∠CFH,
∴OF⊥EO,
∵∠EOB、∠OFC同为∠FOC的余角,
∴∠EOB=∠OFC,
又∠EBO=∠OCF=90°,
∴△EBO∽△OCF,
∴
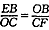 ,
,即EB·CF=OC·OB=a2 ①
∵S1+S2=
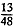 S,
S, ∴
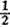 OB·BE+
OB·BE+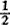 OC·CF=
OC·CF=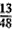 ·4a2,
·4a2,即BE+CF=
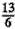 a…②
a…② 解①②得BE=
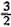 a,FC=
a,FC=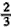 a;或BE=
a;或BE=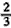 a,FC=
a,FC=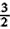 a。
a。 
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.



 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.