题目内容
已知:如图,平面直角坐标系xOy中,点A、B的坐标分别为A(4,0),B(0,-4),P为y轴上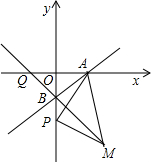 B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.
B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.(1)求直线AB的解析式;
(2)用m的代数式表示点M的坐标;
(3)若直线MB与x轴交于点Q,判断点Q的坐标是否随m的变化而变化,写出你的结论并说明理由.
分析:(1)直线AB的解析式为y=kx+b(k≠0),利用待定系数法求函数的解析式即可;
(2)作MN⊥y轴于点N证得△AOP≌△PNM,得到OP=NM,OA=NP.根据PB=m,用m表示出NM和ON=OP+NP,根据点M在第四象限,表示出点M的坐标即可.
(3)设直线MB的解析式为y=nx-4,根据点M(m+4,-m-8).然后求得直线MB的解析式为,从而得到无论m的值如何变化,点Q的坐标都为(-4,0).
(2)作MN⊥y轴于点N证得△AOP≌△PNM,得到OP=NM,OA=NP.根据PB=m,用m表示出NM和ON=OP+NP,根据点M在第四象限,表示出点M的坐标即可.
(3)设直线MB的解析式为y=nx-4,根据点M(m+4,-m-8).然后求得直线MB的解析式为,从而得到无论m的值如何变化,点Q的坐标都为(-4,0).
解答:解:(1)设直线AB的解析式为y=kx+b(k≠0).
则
解
∴直线AB的解析式为y=x-4.
(2)作MN⊥y轴于点N.
∵△APM为等腰直角三角形,PM=PA,
∴∠APM=90°.
∴∠OPA+∠NPM=90°.
∵∠NMP+∠NPM=90°,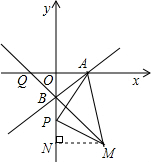
∴∠OPA=∠NMP.
又∵∠AOP=∠PNM=90°,
∴△AOP≌△PNM.(AAS)
∴OP=NM,OA=NP.
∵PB=m(m>0),
∴NM=m+4,ON=OP+NP=m+8.
∵点M在第四象限,
∴点M的坐标为(m+4,-m-8).
(3)答:点Q的坐标不变.
设直线MB的解析式为y=nx-4(n≠0).
∵点M(m+4,-m-8).
在直线MB上,
∴-m-8=n(m+4)-4.
整理,得(m+4)n=-m-4.
∵m>0,
∴m+4≠0.
解得 n=-1.
∴直线MB的解析式为y=-x-4.
∴无论m的值如何变化,点Q的坐标都为(-4,0).
则
|
|
∴直线AB的解析式为y=x-4.
(2)作MN⊥y轴于点N.
∵△APM为等腰直角三角形,PM=PA,
∴∠APM=90°.
∴∠OPA+∠NPM=90°.
∵∠NMP+∠NPM=90°,

∴∠OPA=∠NMP.
又∵∠AOP=∠PNM=90°,
∴△AOP≌△PNM.(AAS)
∴OP=NM,OA=NP.
∵PB=m(m>0),
∴NM=m+4,ON=OP+NP=m+8.
∵点M在第四象限,
∴点M的坐标为(m+4,-m-8).
(3)答:点Q的坐标不变.
设直线MB的解析式为y=nx-4(n≠0).
∵点M(m+4,-m-8).
在直线MB上,
∴-m-8=n(m+4)-4.
整理,得(m+4)n=-m-4.
∵m>0,
∴m+4≠0.
解得 n=-1.
∴直线MB的解析式为y=-x-4.
∴无论m的值如何变化,点Q的坐标都为(-4,0).
点评:本题考查了一次函数的综合知识,本题的综合性强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 BC=4
BC=4 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.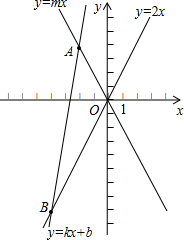 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).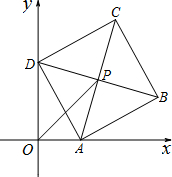 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.