题目内容
已知,如图:平面直角坐标系中,抛物线y=-x2+2x+c的图象与x轴分别交于点A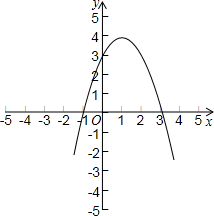 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).(1)求c值;
(2)求直线BC的解析式;
(3)动点M在线段CB上由点C向终点B运动(点M不与点C、B重合),以OM为边在y轴右侧做正方形OMNF.设M点运动速度为
| 2 |
分析:(1)将(2,3)代入抛物线的解析式求出c的值.
(2)设BC的解析式为y=ax+b,将C、D的坐标代入,即可求得a、b的值;
(3)当OM⊥BC时,构不成五边形,因此以此为界限分类讨论,两种情况下思路一样,分别过O、N作BC的垂线,通过构造的全等三角形,来求出△BMN中BM边上的高,然后分别求正方形和三角形的面积即可.
(2)设BC的解析式为y=ax+b,将C、D的坐标代入,即可求得a、b的值;
(3)当OM⊥BC时,构不成五边形,因此以此为界限分类讨论,两种情况下思路一样,分别过O、N作BC的垂线,通过构造的全等三角形,来求出△BMN中BM边上的高,然后分别求正方形和三角形的面积即可.
解答:解:(1)把(2,3)代入y=-x2+2x+c中得c=3;
(2)设BC的解析式为y=ax+b,将C(0,3),B(3,0)代入y=ax+b中,
解得b=3,a=-1,故y=-x+3;
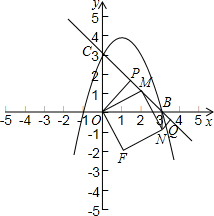
(3)当OM⊥BC时,构不成五边形,因此以此为界限分类讨论,
①当
<t<3时,分别过O、N作BC的垂线,垂足分别为P、Q,则△OPM≌△MQN,PM=NQ,
其中,OP=CP=
,CM=
t,CB=3
,
所以PM=NQ=
t-
,MB=3
-
t,OM=
=
,
所以,正方形OMNF的面积为2t2-6t+9,△BMN的面积为
×BM×NQ=-t2+
t-
,
故五边形面积为s=t2-
t+
;
②当0<t<
,同理可得s=t2-
t+9(0<t<
).
综上所述,s=t2-
t+9(0<t<
),s=t2-
t+
(
<t<3).
(2)设BC的解析式为y=ax+b,将C(0,3),B(3,0)代入y=ax+b中,
解得b=3,a=-1,故y=-x+3;
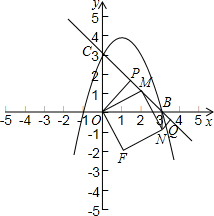
(3)当OM⊥BC时,构不成五边形,因此以此为界限分类讨论,
①当
| 3 |
| 2 |
其中,OP=CP=
3
| ||
| 2 |
| 2 |
| 2 |
所以PM=NQ=
| 2 |
3
| ||
| 2 |
| 2 |
| 2 |
| PM2+OP2 |
| 2t2-6t+9 |
所以,正方形OMNF的面积为2t2-6t+9,△BMN的面积为
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
故五边形面积为s=t2-
| 3 |
| 2 |
| 9 |
| 2 |
②当0<t<
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
综上所述,s=t2-
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
点评:本题考查求一次函数、二次函数的解析式等知识,综合性比较强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 BC=4
BC=4 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.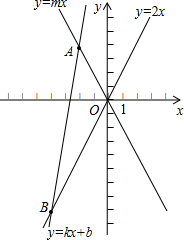 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
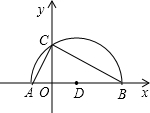
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).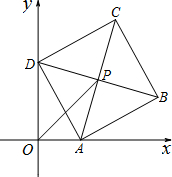 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.