题目内容
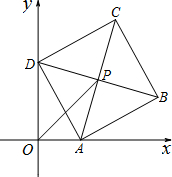 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.(1)当OA=OD时,点D的坐标为
(0,2
)
| 2 |
(0,2
)
,∠POA=| 2 |
45
45
°;(2)当OA<OD时,求证:OP平分∠DOA;
(3)设点P到y轴的距离为d,则在点A,D运动的过程中,d的取值范围是什么?
分析:(1)根据正方形的性质求出△ADP是等腰直角三角形,再判断出△AOD是等腰直角三角形,再求出四边形AODP是正方形,然后根据正方形的性质求出AP=DP=2
,写出点P的坐标即可;
(2)过点P作PM⊥x轴于点M,PN⊥y轴于点N,根据正方形的对角线互相平分且相等可得PD=PA,再根据同角的余角相等求出∠1=∠2,然后利用“角角边”证明△DPN和△APM全等,根据全等三角形对应边相等可得PM=PN,然后利用到角的两边距离相等的点在角的平分线上证明即可;
(3)根据垂线段最短,A、O重合时,点P到y轴的距离最小,为正方形ABCD边长的一半,OA=OD时点P到y轴的距离最大,为PD的长度,即可得解.
| 2 |
(2)过点P作PM⊥x轴于点M,PN⊥y轴于点N,根据正方形的对角线互相平分且相等可得PD=PA,再根据同角的余角相等求出∠1=∠2,然后利用“角角边”证明△DPN和△APM全等,根据全等三角形对应边相等可得PM=PN,然后利用到角的两边距离相等的点在角的平分线上证明即可;
(3)根据垂线段最短,A、O重合时,点P到y轴的距离最小,为正方形ABCD边长的一半,OA=OD时点P到y轴的距离最大,为PD的长度,即可得解.
解答: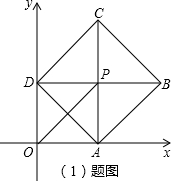 (1)解:∵四边形ABCD为正方形,
(1)解:∵四边形ABCD为正方形,
∴△ADP是等腰直角三角形,
又∵OA=OD,
∴△AOD是等腰直角三角形,
∴四边形AODP是正方形,
∵正方形ABCD的边长为4,
∴AC=BD=
=4
,
∴AP=DP=
×4
=2
,
∴点P的坐标为(0,2
),∠POA=45°;
(2)证明:如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,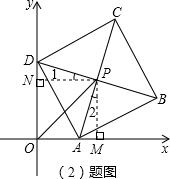
∵四边形ABCD是正方形,
∴PD=PA,∠DPA=90°,
∵PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PMO=∠PNO=∠PND=90°,
∵∠NOM=90°,
∴四边形NOMP中,∠NPM=90°,
∴∠DPA=∠NPM,
∵∠1=∠DPA-∠NPA,∠2=∠NPM-∠NPA,
∴∠1=∠2,
∵在△DPN和△APM中,
,
∴△DPN≌△APM(AAS),
∴PN=PM,
∴OP平分∠DOA;
(3)解:当A、O重合时,点P到y轴的距离最小,
d=
×4=2,
当OA=OD时,点P到y轴的距离最大,d=PD=2
,
∵点A,D都不与原点重合,
∴2<d≤2
.
 (1)解:∵四边形ABCD为正方形,
(1)解:∵四边形ABCD为正方形,∴△ADP是等腰直角三角形,
又∵OA=OD,
∴△AOD是等腰直角三角形,
∴四边形AODP是正方形,
∵正方形ABCD的边长为4,
∴AC=BD=
| 42+42 |
| 2 |
∴AP=DP=
| 1 |
| 2 |
| 2 |
| 2 |
∴点P的坐标为(0,2
| 2 |
(2)证明:如图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,

∵四边形ABCD是正方形,
∴PD=PA,∠DPA=90°,
∵PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PMO=∠PNO=∠PND=90°,
∵∠NOM=90°,
∴四边形NOMP中,∠NPM=90°,
∴∠DPA=∠NPM,
∵∠1=∠DPA-∠NPA,∠2=∠NPM-∠NPA,
∴∠1=∠2,
∵在△DPN和△APM中,
|
∴△DPN≌△APM(AAS),
∴PN=PM,
∴OP平分∠DOA;
(3)解:当A、O重合时,点P到y轴的距离最小,
d=
| 1 |
| 2 |
当OA=OD时,点P到y轴的距离最大,d=PD=2
| 2 |
∵点A,D都不与原点重合,
∴2<d≤2
| 2 |
点评:本题考查了正方形的性质,坐标与图形的性质,全等三角形的判定与性质,角平分线的判定,(2)作辅助线构造出全等三角形是解题的关键,(2)根据垂线段最短判断出最小与最大值的情况是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
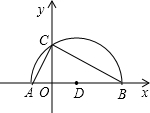 BC=4
BC=4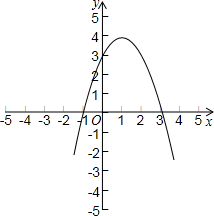 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.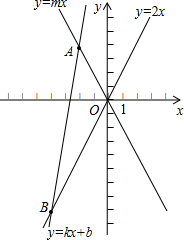 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).