题目内容
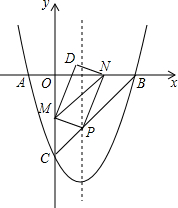
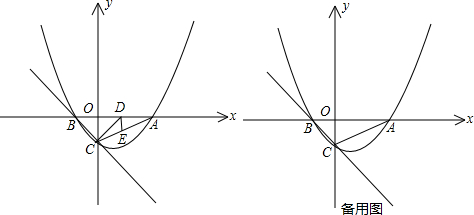
如图,已知抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)和C(0,-3),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.连结MN,设MC=m.
(1)求抛物线的函数解析式;
(2)用含m的代数式表示△PMN的面积S,并求S的最大值;
(3)以PM、PN为一组邻边作矩形PMDN,当此矩形全部落在抛物线与x轴围成的封闭区域内(含边界)时,求m的取值范围.
(1)求抛物线的函数解析式;
(2)用含m的代数式表示△PMN的面积S,并求S的最大值;
(3)以PM、PN为一组邻边作矩形PMDN,当此矩形全部落在抛物线与x轴围成的封闭区域内(含边界)时,求m的取值范围.

(1)∵抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)和C(0,-3),
∴
,
解得:
,
∴抛物线的解析式是y=x2-2x-3;
(2)作PE⊥y轴于点E,设抛物线的对称轴与x轴相交于点F,
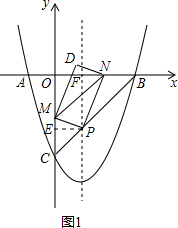 易得抛物线的对称轴为直线x=1,直线BC的解析式为y=x-3,
易得抛物线的对称轴为直线x=1,直线BC的解析式为y=x-3,
∴P(1,-2),
∴E(0,-2),ME=|m-1|,
∴PM=
=
,
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
又∵∠PEM=∠PFN=90°,
∴△MPE∽△NPF,
∴
=
,
∴PN=2PM,
∴S=
PM•PN=m2-2m+2,
∵0≤m≤3,
∴当m=3时,S有最大值,最大值是5;
(3)①当点D在x轴上时,点D、M显然分别与点O、E重合,
此时,m=1;
②当点D在抛物线上时(如图2),作DG⊥x轴于点G,
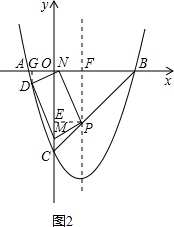 ∠MPE+∠NPE=90°,∠NPE+∠NPF=90°,
∠MPE+∠NPE=90°,∠NPE+∠NPF=90°,
∴∠MPE=∠NPF,
又∵∠DNG+∠PNF=90°,∠NPF+∠PNF=90°,
∴∠DNG=∠NPF,
∴∠MPE=∠DNG,
在△MPE和△DNG中,
,
∴△MPE≌△DNG(AAS),
∴DG=ME=1-m,NG=PE=1,
由(2)得:
=
,故NF=2ME=2-2m,
∴OG=1-ON=NF=2-2m,
∴D(2m-2,m-1),
代入抛物线解析式得:m-1=(2m-2)2-2(2m-2)-3,
整理得:4m2-13m+6=0,
解得:m1=
,m2=
(不合题意,舍去),
∴m=
时,点D恰好在抛物线上,
∴当
≤m≤1时,此矩形全部落在抛物线与x轴围成的封闭区域内.
∴
|
解得:
|
∴抛物线的解析式是y=x2-2x-3;
(2)作PE⊥y轴于点E,设抛物线的对称轴与x轴相交于点F,
 易得抛物线的对称轴为直线x=1,直线BC的解析式为y=x-3,
易得抛物线的对称轴为直线x=1,直线BC的解析式为y=x-3,∴P(1,-2),
∴E(0,-2),ME=|m-1|,
∴PM=
| PE2+ME2 |
| m2-2m+2 |
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
又∵∠PEM=∠PFN=90°,
∴△MPE∽△NPF,
∴
| PN |
| PM |
| PF |
| PE |
∴PN=2PM,
∴S=
| 1 |
| 2 |
∵0≤m≤3,
∴当m=3时,S有最大值,最大值是5;
(3)①当点D在x轴上时,点D、M显然分别与点O、E重合,
此时,m=1;
②当点D在抛物线上时(如图2),作DG⊥x轴于点G,
 ∠MPE+∠NPE=90°,∠NPE+∠NPF=90°,
∠MPE+∠NPE=90°,∠NPE+∠NPF=90°,∴∠MPE=∠NPF,
又∵∠DNG+∠PNF=90°,∠NPF+∠PNF=90°,
∴∠DNG=∠NPF,
∴∠MPE=∠DNG,
在△MPE和△DNG中,
|
∴△MPE≌△DNG(AAS),
∴DG=ME=1-m,NG=PE=1,
由(2)得:
| NF |
| ME |
| PF |
| PE |
∴OG=1-ON=NF=2-2m,
∴D(2m-2,m-1),
代入抛物线解析式得:m-1=(2m-2)2-2(2m-2)-3,
整理得:4m2-13m+6=0,
解得:m1=
13-
| ||
| 8 |
13+
| ||
| 8 |
∴m=
13-
| ||
| 8 |
∴当
13-
| ||
| 8 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 且与OE平行,现正方形以每秒
且与OE平行,现正方形以每秒