题目内容
如图,已知抛物线y=
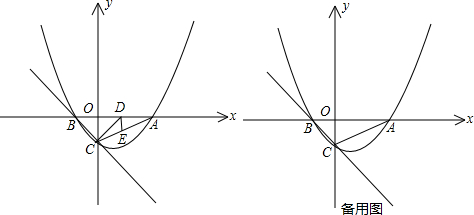
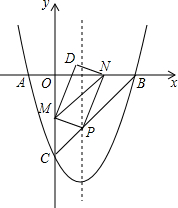
x2+bx+c与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
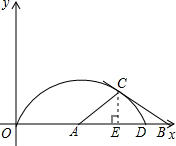
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连接DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连接DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由.

(1)由于抛物线经过A(2,0),C(0,-1),
则有:
,
解得
;
∴抛物线的解析式为:y=
x2-
x-1.
(2)∵A(2,0),C(0,-1),
∴直线AC:y=
x-1;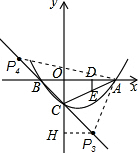
设D(x,0),则E(x,
x-1),
故DE=0-(
x-1)=1-
x;
∴△DCE的面积:S=
DE×|xD|=
×(1-
x)×x=-
x2+
x=-
(x-1)2+
,
因此当x=1,
即D(1,0)时,△DCE的面积最大,且最大值为
.
(3)由(1)的抛物线解析式易知:B(-1,0),
可求得直线BC的解析式为:y=-x-1;
设P(x,-x-1),因为A(2,0),C(0,-1),则有: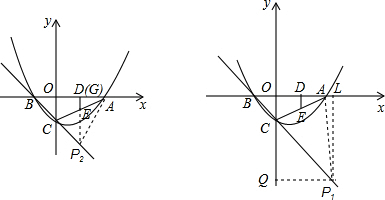
AP2=(x-2)2+(-x-1)2=2x2-2x+5,
AC2=5,CP2=x2+(-x-1+1)2=2x2;
①当AP=CP时,AP2=CP2,有:
2x2-2x+5=2x2,解得x=2.5,
∴P1(2.5,-3.5);
②当AP=AC时,AP2=AC2,有:
2x2-2x+5=5,解得x=0(舍去),x=1,
∴P2(1,-2);
③当CP=AC时,CP2=AC2,有:
2x2=5,解得x=±
,
∴P3(
,-
-1),P4(-
,
-1);
综上所述,存在符合条件的P点,且P点坐标为:P1(2.5,-3.5)、P2(1,-2)、P3(
,-
-1)、P4(-
,
-1).
则有:
|
解得
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵A(2,0),C(0,-1),
∴直线AC:y=
| 1 |
| 2 |

设D(x,0),则E(x,
| 1 |
| 2 |
故DE=0-(
| 1 |
| 2 |
| 1 |
| 2 |
∴△DCE的面积:S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
因此当x=1,
即D(1,0)时,△DCE的面积最大,且最大值为
| 1 |
| 4 |
(3)由(1)的抛物线解析式易知:B(-1,0),
可求得直线BC的解析式为:y=-x-1;
设P(x,-x-1),因为A(2,0),C(0,-1),则有:
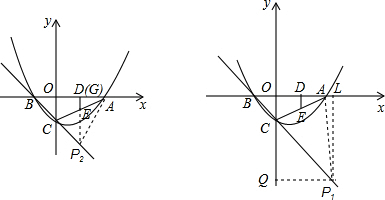
AP2=(x-2)2+(-x-1)2=2x2-2x+5,
AC2=5,CP2=x2+(-x-1+1)2=2x2;
①当AP=CP时,AP2=CP2,有:
2x2-2x+5=2x2,解得x=2.5,
∴P1(2.5,-3.5);
②当AP=AC时,AP2=AC2,有:
2x2-2x+5=5,解得x=0(舍去),x=1,
∴P2(1,-2);
③当CP=AC时,CP2=AC2,有:
2x2=5,解得x=±
| ||
| 2 |
∴P3(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
综上所述,存在符合条件的P点,且P点坐标为:P1(2.5,-3.5)、P2(1,-2)、P3(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目


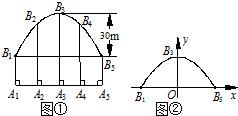
 竹篱笆围成,竹篱笆的长为40m,读九年级的儿子小军为他设计了如下方案:如图,把养鸡场围成等腰梯形ABCD,且∠ABC=120°.
竹篱笆围成,竹篱笆的长为40m,读九年级的儿子小军为他设计了如下方案:如图,把养鸡场围成等腰梯形ABCD,且∠ABC=120°.