题目内容
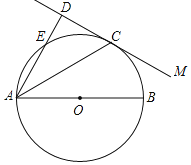
【题目】如图,AB是![]() 的一条弦,点C是
的一条弦,点C是![]() 上一动点,且
上一动点,且![]() ,点E、F分别是AC、BC的中点,直线EF与
,点E、F分别是AC、BC的中点,直线EF与![]() 交于G、H两点.若
交于G、H两点.若![]() 的半径为5,则
的半径为5,则![]() 的最大值为______.
的最大值为______.

【答案】7.5
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为5,可得AB=OA=OB=5,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
如图1,连接OA、OB,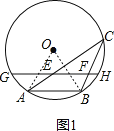 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵⊙O的半径为5,
∴AB=OA=OB=5,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=
AB=![]() ,
,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵当弦GH是圆的直径时,它的最大值为:5×2=10,
∴GE+FH的最大值为:10-![]() =7.5.
=7.5.
故答案为:7.5.

【题目】 某水果公司以3元/kg的成本价新进10000kg柑橘,如果公司希望这批柑橘能获得利润6000元,已知柑橘损坏率统计表如下,请你填写最后一栏数据,完成此表:
(1)损坏率的概率约是多少,并说明理由 (保留小数点后一位)
(2)在出售柑橘(去掉损坏的柑橘)时,确定大约定价多少合适?
柑橘总质量 | 损坏柑橘质量 | 柑橘损坏的频率 |
300 | 30.9 | 0.103 |
350 | 35.7 | 0.102 |
400 | 39.2 | 0.098 |
450 | 44.5 | 0.099 |
500 | 50.5 | ? |
【题目】世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(℉),两种计量之间有如下的对应表:
摄氏温度(℃) | 0 | 10 | 20 | 30 | 40 | 50 |
华氏温度(℉) | 32 | 50 | 68 | 86 | 104 | 122 |
由上表可以推断出,华氏0度对应的摄氏温度是_____℃,若某一温度时华氏温度的值与对应的摄氏温度的值相等,则此温度为_____℃.