Question

【题目】如图，AD是△ABC的高，E为AC上一点，BE交AD于H，且有BH=AC，HD=CD．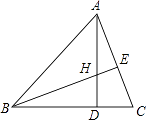
求证：
（1）△BHD≌△ACD；
（2）BE⊥AC．

Answer 1

【答案】
（1）证明：∵AD⊥BC，

∴∠ADB=∠ADC=90°，

在△ADC和△BDH中，

，

∴△ADC≌△BDH（HL）

（2）证明：∵△ADC≌△BDH，

∴∠EBC=∠DAC．

又∵∠DAC+∠ACD=90°，

∴∠EBC+∠ACD=90°，

∴∠BEC=90°，

∴BE⊥AC

【解析】（1）因为AD为△ABC上的高，所以∠ADB=∠ADC=90°，又因为BH=AC，HD=CD，则可根据HL判定△ADC≌△BDF；（2）因为△ADC≌△BDH，则有∠EBC=∠DAC，又因为∠DAC+∠ACD=90°，所以∠EBC+∠ACD=90°，则BE⊥AC．