题目内容
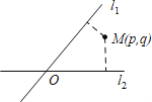
【题目】如图,点 P 是∠AOB 内部一定点

(1)若∠AOB=50°,作点 P 关于 OA 的对称点 P1,作点 P 关于 OB 的对称点 P2,连 OP1、OP2,则∠P1OP2=___.
(2)若∠AOB=α,点 C、D 分别在射线 OA、OB 上移动,当△PCD 的周长最小时,则∠CPD=___(用 α 的代数式表示).
【答案】100° 180°-2α
【解析】
(1)根据对称性证明∠P1OP2=2∠AOB,即可解决问题;
(2)如图,作点P关于OA的对称点P1,作点P关于OB的对称点P2,连P1P2交OA于C,交OB于D,连接PC,PD,此时△PCD的周长最小.利用(1)中结论,根据对称性以及三角形内角和定理即可解决问题;
(1)如图,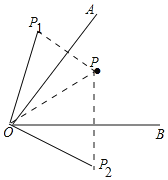
由对称性可知:∠AOP=∠AOP1,∠POB=∠BOP2,
∴∠P1OP2=2∠AOB=100°,
故答案为100°.
(2)如图,作点P关于OA的对称点P1,作点P关于OB的对称点P2,连P1P2交OA于C,交OB于D,连接PC,PD,此时△PCD的周长最小.
根据对称性可知:∠OP1C=∠OPC,∠OP2D=∠OPD,∠P1OP2=2∠AOB=2α.
∴∠CPD=∠OP1C+∠OP2D=180°-2α.
故答案为180°-2α.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目