��Ŀ����
����Ŀ��ֱ��y=��x+6��x�ύ��A����y�ύ��B��ֱ��CD��y�ύ��C��0��2����ֱ��AB����D����D��DE��x����E��3��0����
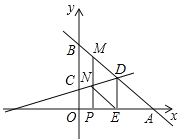
��1����ֱ��CD�ĺ�������ʽ��
��2��P���߶�OA��һ���㣬��P��ԭ��O��ʼ��ÿ��һ����λ���ȵ��ٶ���A�˶���P��O��A���غϣ�����P��x��Ĵ��ߣ��ֱ���ֱ��AB��CD����M��N����MN�ij�ΪS��P���˶���ʱ��Ϊt�����S��t֮��ĺ�����ϵʽ��д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£���tΪ��ֵʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ���ֱ��д�������
���𰸡���1��y= ![]() x+2����2��MN=|��
x+2����2��MN=|�� ![]() +4|(0<t<6)��3��
+4|(0<t<6)��3��![]() ��
�� ![]() ��
��
����������1���������������D�������������ô���ϵ���������ֱ��CD�ĺ�������ʽ��
��2����t�ɷֱ��ʾ��M��N����������ɱ�ʾ��S��t֮��Ĺ�ϵʽ��
��3����������֪MN��DE������ƽ���ı��ε����ʿ�֪MN=DE���ɣ�2���Ĺ�ϵʽ�ɵõ�����t�ķ����������t��ֵ��
��1����ֱ��CD��y���ཻ�ڣ�0��2���������ֱ��CD����ʽΪy=kx+2����x=3����y=��x+6�пɵ���y=3����D��3��3������D���������y=kx+2�пɵ�3=3k+2�������k=![]() ����ֱ��CD�ĺ�������ʽΪy=
����ֱ��CD�ĺ�������ʽΪy=![]() x+2��
x+2��
��2���������֪OP=t����x=t����y=��x+6�пɵ���y=��t+6����M��t����t+6������x=t����y=![]() x+2�пɵ���y=
x+2�пɵ���y=![]() t+2����N��t��
t+2����N��t��![]() t+2������MN=|��t+6����
t+2������MN=|��t+6����![]() t+2��|=|��
t+2��|=|��![]() +4|��
+4|��
�ߵ�P���߶�OA������A��6��0������0��t��6����MN=|�� ![]() +4|(0��t��6)��
+4|(0��t��6)��
��3���������֪MN��DE��
����M��N��E��DΪ������ı�����ƽ���ı�������MN=DE=3����|��![]() +4|=3�������t=
+4|=3�������t=![]() ��t=
��t=![]() ��
��
����t��ֵΪ![]() ��
��![]() ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�
ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�

����Ŀ��ijУΪ���˽���꼶ѧ������450�ˣ����������������������ʦ�Ծţ�1�����50λѧ������һ���������������ԣ��Բ�������Ϊ���������������²���Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��
��� | ����x | Ƶ���������� |
A | 80��x��100 | 6 |
B | 100��x��120 | 8 |
C | 120��x��140 | m |
D | 140��x��160 | 18 |
E | 160��x��180 | 6 |
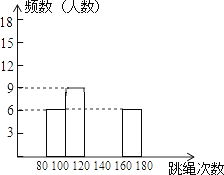
����ͼ������������⣺
��1�����е�m=________��
��2�����Ƶ���ֲ�ֱ��ͼ��������
��3������������ݵ���λ�����ڵ�________�飻
��4�������꼶ѧ��һ��������������x���ϸ�Ҫ����x��120������ƾ��꼶ѧ����һ���������ɼ����ϸ��������