题目内容
【题目】如图，在△ABC中，∠B＝30°，∠C＝50°，AE是∠BAC的平分线，AD是高．
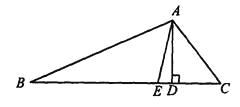
(1)求∠BAE的度数；
(2)求∠EAD的度数．
【答案】∠BAE为50°,∠EAD为10°。
【解析】
试题（1）根据△ABC的内角和定理求得∠BAC=100°；然后由角平分线的性质、△ABE的内角和定理来求∠BAE的度数；
（2）由三角形内角和定理可求得∠BAC的度数，在Rt△ADC中，可求得∠DAC的度数，AE是角平分线，有∠EAC=
∠BAC，故∠EAD=∠EAC-∠DAC．
解：（1）∵在△ABC中，∠B=30°，∠C=50°，
∴∠BAC=180°-∠B-∠C=100°；
又∵AE是∠BAC的平分线，
∴∠BAE=∠BAC=50°；
（2）∵AD是边BC上的高，
∴∠ADC=90°，
∴在△ADC中，∠C=50°，∠C+∠DAC=90°，
∴∠DAC=40°，
由（1）知，∠BAE=∠CAE=50°，
∴∠DAE=∠EAC-∠DAC=50°-40°=10°，即∠EAD=10°
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
.
【解析】试题分析：
根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.
试题解析：
列表如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （1，2） | （1，3） | （1，4） |
2 | （2，1） | （2，2） | （2，3） | （2，4） |
3 | （3，1） | （3，2） | （3，3） | （3，4） |
4 | （4，1） | （4，2） | （4，3） | （4，4） |
由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，
∴P（两次摸到小球的数字之和等于4）=
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．
