题目内容
【题目】如图，抛物线y=﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为 ． 
【答案】（1+ 
，2）或（1﹣ ，2）
【解析】解： ∵△PCD是以CD为底的等腰三角形，
∴点P在线段CD的垂直平分线上，
如图，过P作PE⊥y轴于点E，则E为线段CD的中点，
∵抛物线y=﹣x2+2x+3与y轴交于点C，
∴C（0，3），且D（0，1），
∴E点坐标为（0，2），
∴P点纵坐标为2，
在y=﹣x2+2x+3中，令y=2，可得﹣x2+2x+3=2，解得x=1± ，
∴P点坐标为（1+ ，2）或（1﹣ ，2），
故答案为：（1+ ，2）或（1﹣ ，2）．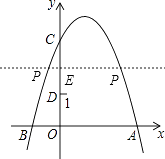
当△PCD是以CD为底的等腰三角形时，则P点在线段CD的垂直平分线上，由C、D坐标可求得线段CD中点的坐标，从而可知P点的纵坐标，代入抛物线解析式可求得P点坐标．
练习册系列答案
相关题目
