题目内容
【题目】如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )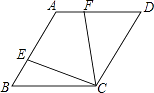
A.120°
B.140°
C.160°
D.180°
【答案】D
【解析】解:连接AC,
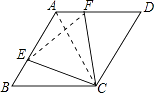
∵在菱形ABCD中,∠B=60°,
∴AC=AB=BC=CD=AD,
∵BE=AF,
∴AE=DF,
∵∠B=60°,AC是对角线,
∴∠BAC=60°,
∴∠BAC=∠D=60°,
∴△ACE≌△CDF,
∴EC=FC.∠ACE=∠DCF,
∵∠DCF+∠ACF=60°,
∴∠ACE+∠ACF=60°,
∴△ECF是等边三角形.
故可得出∠ECF=60°,又∠EAF=120°,
∴∠AEC+∠AFC=360°﹣(60°+120°)=180°.
故答案为:D.
根据菱形的性质,得到四边相等,由∠B=60°,得到△ACE≌△CDF,△ECF是等边三角形,求出∠AEC+∠AFC的值.

练习册系列答案
相关题目