题目内容
【题目】如图,在⊙O中,弦AB、CD互相垂直,垂足为E,点M在CD上,连接AM并延长交BC于点F,交圆上于点G,连接AD,AD=AM.
(1)如图1,求证:AG⊥BC;
(2)如图2,连接EF,DG,求证:EF∥DG;
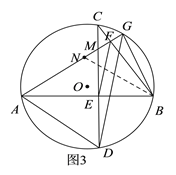
(3)如图3,在(2)的条件下,连接BG,若∠ABG=2∠BAG,EF=15,AB=32,求BG长.

【答案】(1)AG⊥BC;(2)E、F分别为MD、MG中点,EF∥DG ;(3)BG=18
【解析】
试题
(1)由AB⊥CD于点E可得∠B+∠C=90°;由AD=AM,可得∠CMF=∠AMD=∠D=∠B,由此可得∠CMF+∠C=90°,从而得到∠CFM=90°即可得到AG⊥BC;
(2)如图2,连接CG,由AD=AM,AB⊥CD可得点E是DM的中点;由(1)可知∠CMF=∠B,结合∠B=∠CGA,可得∠CMF=∠CGA,从而可得CM=CG,结合(1)中结论AG⊥BC可得点F是MG的中点,由此可得EF是△MDG的中位线,从而可得结论EF∥DG;
(3)如图3,作∠ABG的平分线交AG于点N,由∠ABG=2∠BAG,结合已知条件可证得∠ABG=∠DAG,从而得到AG=DG=2EF=30;由BN平分∠ABG及∠ABG=2∠BAG可得∠GBN=∠ABN=∠GAB,结合∠AGB=∠BGA可证得△GBN∽GAB,BN=AN,设AN=x、BG=y,根据相似三角形的性质列出比例式即可解得BG的值.
试题解析:
(1)∵AB⊥CD于点E,
∴∠BEC=90°,
∴∠B+∠C=90°.
∵AD=AM,
∴∠AMD=∠D=∠B,
又∵∠CMF=∠AMD,
∴∠CMF=∠B,
∴∠CMF+∠C=90°,
∴∠CFM=90°,
∴AG⊥BC;
(2)如图2,连接CG,
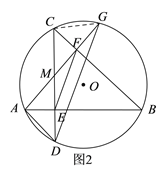
(2)由(1)可知,∠CMF=∠B,
∵∠B=∠CGA,
∴∠CMF=∠G,
∴CM=CG,
又∵AG⊥BC,
∴点F是MG的中点.
∵AD=AM,AB⊥CD,
∴点E是DM的中点,
∴EF是△MDG的中位线,
∴EF∥DG;
(3)∵由(2)可知,EF是△MDG的中位线,EF=15,
∴DG=2EF=30,
∵AD=AM,AB⊥CD,
∴∠DAG=2∠BAG,
又∵∠ABG=2∠BAG,
∴∠ABG=∠DAG,
∴AG=DG=30.
如图3,作BN平分∠ABG,则∠GBN=∠ABN=∠GAB,
∴AN=BN,
∵∠AGB=∠BGA,
∴△GBN∽GAB,
∴![]() ,
,![]() ,
,
设BG=x,AN=BN=y,则GN=AG-AN=30-y,
∴![]() ,
,![]() ,两式变形可得:
,两式变形可得:![]() ,
,
解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴BG=18.

 名校课堂系列答案
名校课堂系列答案