题目内容
【题目】如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
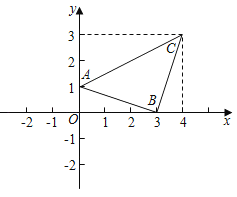
【答案】(1)△ABC是等腰直角三角形,理由详见解析;(2)(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ) .
) .
【解析】
(1)结论:△ABC是等腰直角三角形.添加辅助线,构造全等三角形解决问题;
(2)分三种情形画出图形即可解决问题.
解:(1)结论:△ABC是等腰直角三角形.
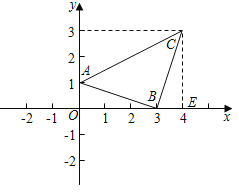
理由:作CE⊥x轴于E.
∵点A(0,1),点B(3,0),点C(4,3),
∴OA=BE=1,OB=CE=3,
∵∠AOB=∠CEB=90°,
∴△AOB≌△BEC(SAS),
∴BA=BC,∠ABO=∠BCE,
∵∠BCE+∠CBE=90°,
∴∠ABO+∠CBE=90°,
∴∠ABC=90°,
∴△ABC是等腰直角三角形.
(2)如图,
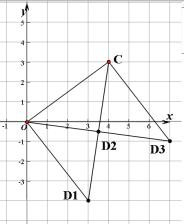
由图象可知:
①当OC为腰,点O为直角顶点时,即OC绕点O顺时针旋转90°,由(1)中正三角形全等的方法,可得D1坐标为(3,﹣4);
②当OC为腰,点C为直角顶点时,即OC绕点C逆时针旋转90°,方法同①,得D3坐标为(7,﹣1;
③当OC是等腰直角三角形的斜边时,因为∠OCD1=∠COD3=45°,所以CD1与OD3的交点即为D2,也是CD1与OD3的中点,可得坐标为(![]() ,﹣
,﹣![]() ).
).
综上:满足条件的点D的坐标分别为(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ).
).
故答案为(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ).
).

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目