题目内容
已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,
E是BC的中点,连结DE.
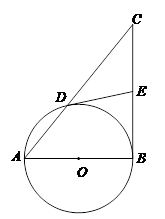
(1)求证:DE与⊙O相切;
(2)连结OE,若cos∠BAD=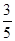 ,BE=
,BE=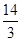 ,求OE的长.
,求OE的长.
E是BC的中点,连结DE.

(1)求证:DE与⊙O相切;
(2)连结OE,若cos∠BAD=
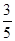 ,BE=
,BE=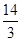 ,求OE的长.
,求OE的长.(1)通过证明: ,证明DE和⊙O相切。(2)
,证明DE和⊙O相切。(2) 。
。
 ,证明DE和⊙O相切。(2)
,证明DE和⊙O相切。(2) 。
。试题分析:(1)证明:如图所示,连接OD,BD

∵AB是⊙O的直径,∴
 ° .
° . 在Rt△BDC中∵E是BC的中点,∴DE=
 BC;
BC;∴DE=BE; ∴
 .
. ∵OD="OB," ∴
 ;
; ∵
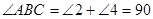 °
°∴
 ° 即OD⊥DE
° 即OD⊥DE∴DE是⊙O的切线
(2)解: ∵
 ,
,
∴△
 ∽ △
∽ △ ∴
∴
∵
 ,
, ∴
∴
∵OE是△ABC的中位线
∴

点评:本题难度中等,主要考查学生对圆和相似三角形知识点的掌握。为中考常见题型,要求学生培养数形结合思想,运用到考试中去。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 的三等分点,
的三等分点,  ,则
,则 的度数为 .
的度数为 . 
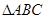 的外接⊙
的外接⊙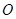 的半径为
的半径为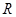 ,高为
,高为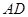 ,
,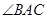 的平分线交⊙
的平分线交⊙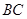 于
于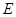 、
、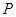 ,
,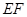 切⊙
切⊙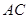 的延长线于
的延长线于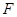 .下列结论:①
.下列结论:①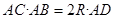 ;②
;②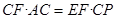 ;④
;④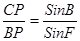 .请你把正确结论的番号都写上 .(填错一个该题得
.请你把正确结论的番号都写上 .(填错一个该题得 分)
分)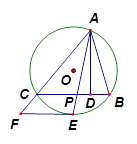
 是
是 的外接圆,
的外接圆, 是
是 ,
, ,则
,则 的值是( )
的值是( )


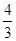
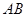 是半圆
是半圆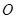 的直径, 点
的直径, 点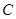 在
在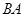 的延长线上运动(点
的延长线上运动(点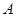 不重合), 以
不重合), 以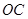 为直径的半圆
为直径的半圆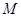 与半圆
与半圆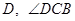 的平分线与半圆
的平分线与半圆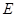 .
.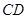 是半圆
是半圆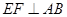 于点
于点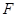 , 猜想
, 猜想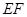 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;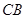 的平行线交
的平行线交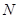 , 当
, 当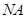 与半圆
与半圆
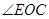 的正切值.
的正切值. ,则这条弦的中点到弦所对优弧的中点的距离为( )
,则这条弦的中点到弦所对优弧的中点的距离为( ) )cm
)cm
