Question

【题目】已知：Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点E在AC上（E与A、C均不重合）．

(1)若点F在AB上，且EF平分Rt△ABC的周长，设AE＝x，用含x的代数式表示

△AEF的面积S△AEF；

(2)若点F在折线ABC上移动，试问是否存在直线EF将Rt△ABC的周长与面积同时平分？若存在直线EF，则求出AE的长；若不存在，请说明理由．

Answer 1

【答案】（1）S△AEF＝（0＜x≤3）；（2）存在直线EF将Rt△ABC的周长与面积同时平分，AE的长是．

【解析】

(1)、根据AE=x得到AF，然后表示出DF，利用三角形的面积列出两个变量之间的关系式即可；(2)、根据EF平分三角形ABC的面积列出有关x的一元二次方程，解得有意义即可判定存在．

（1）如图1，过点F作FM⊥AC于M，

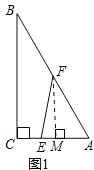
Rt△ABC中，∠C＝90°，AC＝3，BC＝4，得AB＝5，∴△ABC周长为12

EF平分△ABC的周长，AE＝x，可得AE＋AF＝CE＋BC＋BF，

即：x＋AF＝3－x＋4＋5－AF，解得AF＝6－x．

由△AMF∽△ACB可知，

AF∶AB＝FM∶BC，即（6—x）∶5＝FM∶4，

解得FM＝

∴S△AEF＝（0＜x≤3）

（2）若EF存在，

①当F在AB上时，如图1，

则由（1）可知，S△AEF＝，得

化简得，，由，

解得：，（不合题意舍去）．

②当F在BC上时，如图2，

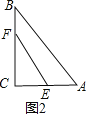
CF＋CE＝AE＋AB＋BF，

即CF＋3－x＝x＋5＋4－CF，

CF＝3＋x，

根据面积平分得出S△CFE＝

∴＝3，得，（舍去），

当时，CF＝3＋x＝3＋＞BC，故舍去

综上所述，即存在直线EF将Rt△ABC的周长与面积同时平分，AE的长是．