题目内容
【题目】如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx﹣3与y轴交于点B.
(1)求直线l的表达式;
(2)若点C是直线l与双曲线![]() 的一个公共点,AB=3AC,求n的值.
的一个公共点,AB=3AC,求n的值.
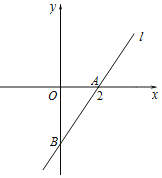
【答案】(1)y![]() x﹣3;(2)n
x﹣3;(2)n![]() 或
或![]() .
.
【解析】
(1)将点A坐标代入直线解析式求得m即可;
(2)先求出点B坐标,再分点C在BA延长线上和点C在线段AB上两种情况,利用相似三角形的判定与性质求出点C的坐标即可.
解:(1)∵直线l:y=mx﹣3过点A(2,0),
∴0=2m﹣3.
∴m![]() .
.
∴直线l的表达式为y![]() x﹣3;
x﹣3;
(2)当x=0时,y=﹣3,
∴点B(0,﹣3),
如图1,当点C在BA延长线上时,作CD⊥y轴于点D,
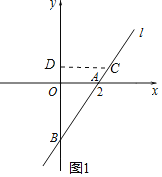
则△BAO∽△BCD,
∴![]() ,即
,即![]() ,
,
解得:CD![]() ,OD=1,
,OD=1,
∴点C(![]() ,1),
,1),
则n![]() 1
1![]() ;
;
如图2,当点C在线段AB上时,作CE⊥y轴于点E,
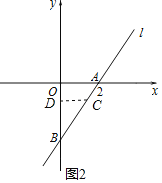
则△BAO∽△BCE,
∴![]() ,即
,即![]() ,
,
解得:CE![]() ,BE=2,
,BE=2,
∴OE=BO﹣BE=1,
∴点C的坐标为(![]() ,﹣1),
,﹣1),
则n![]() (﹣1)
(﹣1)![]() ,
,
综上,n![]() 或
或![]() .
.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目