题目内容
【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长
【答案】
(1)证明:连结AD,如图,
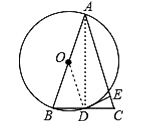
∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∴D为BC的中点,∴BD=CD,∴AB=AC;
(2)证明:连结OD,如图,∵OA=OB,DB=DC,∴OD为△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∴DE是⊙O的切线
(3)解:BD=DC= ![]() BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中,
BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中, ![]() AD*DC=
AD*DC= ![]() AC*DE,∴DE=
AC*DE,∴DE= ![]()
【解析】(1)由AB为⊙O的直径,得到∠ADB=90°,由D为BC的中点,根据等腰三角形的三线合一,得到AB=AC;(2)根据三角形的中位线定理,得到OD⊥DE,得到DE是⊙O的切线;(3)根据勾股定理求出AD的值,根据三角形的面积公式求出DE的值.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?