题目内容
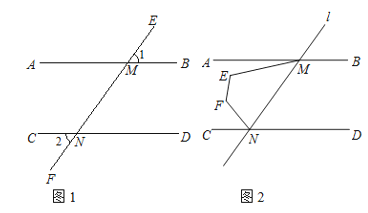
【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
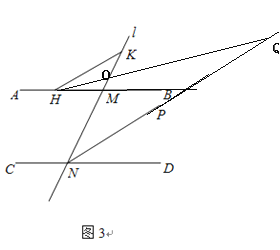
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
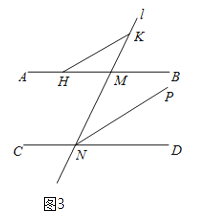
【答案】(1)见解析;(2)∠AME+∠FNC=75°;(3)∠PND-∠QHB=25°或3∠PND-∠QHB=75°
【解析】
(1)根据平行线的判定证出∠2=∠AMF即可;
(2)如图,过E,F分别作EH∥AB,FK∥AB,可得AB∥EH∥FK∥CD,根据平行线的性质即可求解;
(3)分两种情况考虑:HQ在∠KHM内和在∠KHM外,根据平行线的性质和三角形外角的性质分别求出结论即可.
(1)证明:∠1=∠AMF
又∠1=∠2
∴∠2=∠AMF
∴AB∥CD
(2)如图,过E,F分别作EH∥AB,FK∥AB
又AB∥CD ∴AB∥EH∥FK∥CD
∴∠HEF+∠EFK=180°
又∠MEF+∠EFN=255°
∴∠MEH+∠KFN=75°,
∵AB∥EH
∴∠MEH=∠AME,
∵ FK∥CD
∴∠FNC=∠KFN
∴∠AME+∠FNC=75°;

(3)∠PND-∠QHB=25° 或3∠PND-∠QHB=75°
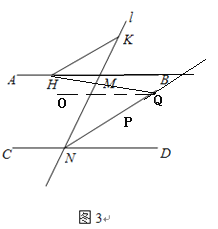
过Q作QO∥AB,则QO∥AB∥CD
∴∠KMB=∠MND=2∠PND,∠OQN=∠PND,∠OQH=∠MHQ
∴∠HQN=∠PND+∠MHQ
∠HKN=∠KMB-∠KHM=2∠PND-2∠MHQ
∵∠HQN+∠HKN=75°,
∴2∠PND-2∠MHQ+∠PND+∠MHQ=75°,即3∠PND-∠QHB=75°;
如图,∠HKN=∠KMB-∠KHM=2∠PND-2∠MHQ
∠HOM=∠OMB-∠MHQ=2∠PND-∠MHQ
∠HQN=∠HOM-∠MNB=∠HOM-∠PND=2∠PND-∠MHQ-∠PND=∠PND-∠MHQ
∵∠HQN+∠HKN=75°,
∴∠PND-∠MHQ+2∠PND-2∠MHQ=75°,即∠PND-∠QHB=25°.
故答案为:(1)见解析;(2)∠AME+∠FNC=75°;(3)∠PND-∠QHB=25°或3∠PND-∠QHB=75°.

 名校课堂系列答案
名校课堂系列答案