��Ŀ����
����Ŀ����ͼ��ֱ��l����A��B���㣬��O���߶�AB�ϵ�һ�㣬��OA=10cm��OB=5cm��
��1������C���߶� AB ���е㣬���߶�CO�ij���
��2�������� P��Q �ֱ�� A��B ͬʱ�����������˶�����P���ٶ�Ϊ4cm/s����Q���ٶ�Ϊ3cm/s�����˶�ʱ��Ϊ x �룬
�ٵ� x=__________��ʱ��PQ=1cm��
������M�ӵ�O��7cm/s���ٶ���P��Q����ͬʱ�����˶����Ƿ���ڳ���m��ʹ��4PM+3OQ��mOMΪ��ֵ�������������mֵ�Լ������ֵ���������ڣ���˵�����ɣ�
��3�������������� OC��OD ��������OAͬʱ�Ƶ�O˳ʱ�뷽����ת��OC��ת���ٶ�Ϊ6��/�룬OD ��ת���ٶ�Ϊ2��/��.��OC��OD��һ���غ�ʱ��OC��OD ͬʱֹͣ��ת������תʱ��Ϊt�룬��tΪ��ֵʱ������ OC��OD��

���𰸡���1��CO=2.5����2����14��16 ���ڶ�ֵ55�����ɼ���������3��t=22.5��67.5
��������
��1��������߶�AB�ij���Ȼ������߶��е�Ķ�������
��2������PQ=1���õ�|15-��4x-3x��|=1���ⷽ�̼��ɣ�
���ȱ�ʾ��PM��OQ��OM�ij�������4PM+3OQ��mOM�õ�55+��21-7m��x��Ҫʹ4PM+3OQ��mOMΪ��ֵ����21-7m=0���ⷽ�̼��ɣ�
��3��������������ۣ�����ͼ�Σ�����ͼ���г����̣��ⷽ�̼��ɣ�
��1����OA=10cm��OB=5cm����AB=OA+OB=15cm��
����C���߶� AB ���е㣬��AC=![]() AB=7.5cm����CO=AO-AC=10-7.5=2.5��cm����
AB=7.5cm����CO=AO-AC=10-7.5=2.5��cm����
��2���١�PQ=1����|15-��4x-3x��|=1����|15-x|=1����15-x=��1����ã�x=14��16��
�ڡ�PM=10+7x-4x=10+3x��OQ=5+3x��OM=7x����4PM+3OQ��mOM=4��10+3x��+3��5+3x��-7mx=55+��21-7m��x��Ҫʹ4PM+3OQ��mOMΪ��ֵ����21-7m=0����ã�m=3����ʱ��ֵΪ55��
��3���������������������ͼ1�������������6t-2t=90�������t=22.5��
����ͼ2�������������6t+90=360+2t�������t=67.5��
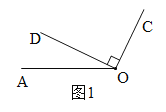
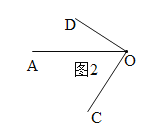
������������t=22.5���67.5��ʱ������ OC��OD��

 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�����Ŀ��������������ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С����������һ��С�γ�����������¼��7����ÿ����ʻ��·�̣����������50kmΪ��������50km�ļ�Ϊ��+��������50km�ļ�Ϊ���������պ�50km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·�̣�km�� | ��8 | ��11 | ��14 | 0 | ��16 | +41 | +8 |
��1�������������ƽ��ÿ����ʻ����ǧ�ף�
��2����ÿ��ʻ100km��������6�������ͼ�6.2Ԫ/���������С����һ���£���30��ƣ������ͷ����Ƕ���Ԫ��





