题目内容
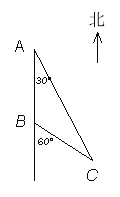
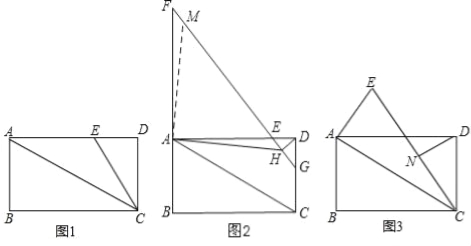
【题目】如图,四边形ABCD为矩形,连接AC,AD=2CD,点E在AD边上.
(1)如图1,若∠ECD=30°,CE=4,求△AEC的面积;
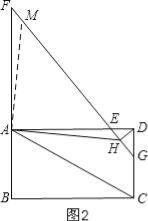
(2)如图2,延长BA至点F使得AF=2CD,连接FE并延长交CD于点G,过点D作DH⊥EG于点H,连接AH,求证:FH=![]() AH+DH;
AH+DH;
(3)如图3,将线段AE绕点A旋转一定的角度α(0°<α<360°)得到线段AE′,连接CE′,点N始终为CE′的中点,连接DN,已知CD=AE=4,直接写出DN的取值范围.
【答案】(1)12﹣2![]() ;(2)证明见解析(3)2
;(2)证明见解析(3)2![]() <DN≤2
<DN≤2![]()
【解析】
试题分析:(1)根据30°的直角三角形求CD和ED,再利用面积公式求△AEC的面积;
(2)作辅助线,构建全等三角形,证明△AFM≌△ADH,得AM=AH,FM=DH,则△MAH是等腰直角三角形,有MH=![]() AH,根据线段的和代入得结论;
AH,根据线段的和代入得结论;
(3)根据将线段AE绕点A旋转一定的角度α(0°<α<30°)得到线段AE′,先计算当AE旋转时DN的最小值和最大值,当α=0°时,DN最小;当α=180°时,DN最大,分别计算,写出结论.
试题解析:(1)在Rt△EDC中,∵∠EDC=30°,
∴ED=![]() EC=
EC=![]() ×4=2,cos30°=
×4=2,cos30°=![]() ,
,
∴DC=ECcos30°=4×![]() =2
=2![]() ,
,
∴AE=2DC﹣ED=4![]() ﹣2,
﹣2,
∴![]() =
=![]() ×AE×DC=
×AE×DC=![]() (4
(4![]() ﹣2)×2
﹣2)×2![]() =12﹣2
=12﹣2![]() ;
;
(2)过A作AM⊥AH,交FG于M,
∴∠MAH=∠MAD+∠DAH=90°,
又∵∠FAD=∠MAD+∠FAM=90°,
∴∠FAM=∠DAH,
∵AF∥CD,
∴∠F=∠FGD
∵DH⊥EG,
∴∠DHE=∠HDG+∠FGD=90°,
∠EDG=∠EDH+∠HDG=90°,
∴∠FGD=∠EDH,
∴∠F=∠EDH,
又∵AF=2CD,AD=2CD,
∴AF=AD,
∴△AFM≌△ADH,
∴AM=AH,FM=DH,
∴△MAH是等腰直角三角形,
∴MH=![]() AH,
AH,
∵FH=MH+FM,
∴FH=![]() AH+DH;
AH+DH;
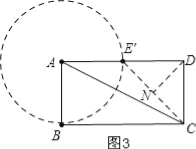
(3)∵线段AE绕点A旋转一定的角度α(0°<α<306°)得到线段AE′,
当α=0°时,点E′在AD中点,如图3,
∵四边形ABCD为矩形,CD=AE=4,AD=2CD,
∴∠CDE′=90°,DE′=CD=4,
∴△CDE′是等腰三角形,
又∵N是CE′的中点,
∴CE′⊥DN,
此时DN的值最小为2![]() ;
;
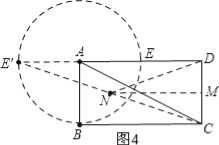
当α=180°时,E′在AD的延长线上,DN最长,
过N作CD垂线交CD于点M,
∵DE′=AE′+AD=12,CD=4,
∵MN⊥DC,DE′⊥DC,
∴MN∥DE′,
∴△CDE′∽△CMN,
∴![]() =
=![]() ,
,
∴MN=6,
则CM=DM=2,
∴在Rt△DMN中,DN=![]() =2
=2![]() ,
,
∵0°<α<360°
∴2![]() <DN≤2
<DN≤2![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案