题目内容
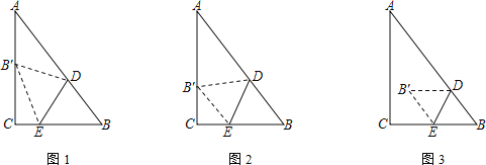
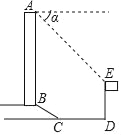
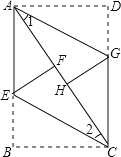
【题目】如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形:
(2)若AB=8cm,BC=6cm,求线段EF的长.
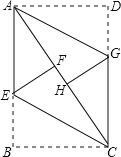
【答案】(1)证明见解析;(2)EF=3cm.
【解析】
(1)根据矩形的性质和折叠的性质求得AB∥CD,AG∥CE,即可证明四边形AECG是平行四边形;
(2)根据勾股定理求出AC的长,再根据CF=BC求出AF的长,设EF=BE=x,则AE=8﹣x,由勾股定理得EF2+AF2=AE2,代入求出x的值即可.
(1)∵四边形ABCD是矩形,
∴AB∥CD,AD∥BC,
∴∠DAC=∠BCA.
由折叠可知∠1![]() ,∠2
,∠2![]() ,
,
∴∠1=∠2,
∴AG∥CE,
又∵AE∥CG,
∴四边形AECG是平行四边形;
(2)在Rt△ABC中,∠B=90°,AB=8cm,BC=6cm,
由勾股定理可得:AC![]() 10,
10,
又∵CF=BC,
则AF=AC﹣CF=4.
设EF=BE=x,则AE=8﹣x,
在Rt△AFE中,由勾股定理得EF2+AF2=AE2,
即x2+42=(8﹣x)2,
解得:x=3,
即EF=3cm.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.