题目内容
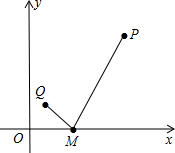如图，在直角坐标系中，点M（x，0）可在x轴上运动，且它到点P（5，5），Q（2，1）的距离分别为MP和MQ，当MP+MQ的值最小时，求点M的坐标．
分析：作P点关于x 的对称点P′，根据轴对称的性质，PM=P′M，MP+MQ的最小值可转化为QP′的最小值，再求出P′Q所在的直线的解析式，即可求出直线与x轴的交点．
解答：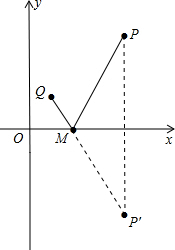
解：作P点关于x 的对称点P′，
∵P点的坐标为（5，5），
∴P′（5，-5）PM=P′M，
连接P′Q，则P′Q与x轴的交点应为满足QM+PM的值最小，
即为M点．
设P′Q所在的直线的解析式为：y=kx+b，
于是有方程组
，
解得：
．
∴y=-2x+5，
当y=0时，x=
，
∴M（
，0）
解：作P点关于x 的对称点P′，∵P点的坐标为（5，5），
∴P′（5，-5）PM=P′M，
连接P′Q，则P′Q与x轴的交点应为满足QM+PM的值最小，
即为M点．
设P′Q所在的直线的解析式为：y=kx+b，
于是有方程组
|
解得：
|
∴y=-2x+5，
当y=0时，x=
| 5 |
| 2 |
∴M（
| 5 |
| 2 |
点评：本题考查了轴对称---最短路径问题和待定系数法求一次函数解析式，明确轴对称的定义，会将最小值问题转化为轴对称的问题是解题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：