题目内容
如图，已知?ABCD和?AB′C′D有一条公共边AD，它们的对边在同一条直线上．
（1）求证：△ABB′≌△DCC′；
（2）若∠1=∠2，求证：四边形ABC′D为等腰梯形．
证明：（1）由题意可得，AB=CD，AB′=DC′，且BB′=CC′，所以△ABB′≌△DCC′；
（2）由（1）可得，∠ABB′=∠DCC′，
∵∠1=∠2
∴∠B=∠C′，
又AD∥BC，
∴四边形ABC′D为等腰梯形．
分析：（1）三边对应相等可证明其全等，
（2）在（1）的条件下，再证明∠B=∠C′，即可得到四边形ABC?D为等腰梯形
点评：熟练掌握三角形全等性质的判定，掌握等腰梯形的性质．
（2）由（1）可得，∠ABB′=∠DCC′，
∵∠1=∠2
∴∠B=∠C′，
又AD∥BC，
∴四边形ABC′D为等腰梯形．
分析：（1）三边对应相等可证明其全等，
（2）在（1）的条件下，再证明∠B=∠C′，即可得到四边形ABC?D为等腰梯形
点评：熟练掌握三角形全等性质的判定，掌握等腰梯形的性质．
练习册系列答案
名校课堂系列答案
相关题目
14、如图，已知?ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是
26、如图，已知?ABCD，AE平分∠BAD，交DC于E，DF⊥BC于F，交AE于G，且DF=AD．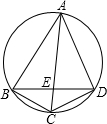
如图，已知ABCD是圆的内接四边形，对角线AC和BD相交于E，BC=CD=4，AE=6，如果线段BE和DE的长都是整数，则BD的长等于
如图，已知ABCD是圆O的内接四边形，AB=BD，BM⊥AC于M，求证：AM=DC+CM．