题目内容
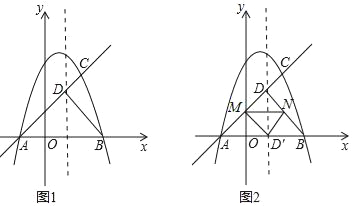
【题目】如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B两点，（点A在点B的左侧），与直线AC交于点C（2，3），直线AC与抛物线的对称轴l相交于点D，连接BD．
（1）求抛物线的函数表达式，并求出点D的坐标；
（2）如图2，若点M、N同时从点D出发，均以每秒1个单位长度的速度分别沿DA、DB运动，连接MN，将△DMN沿MN翻折，得到△D′MN，判断四边形DMD′N的形状，并说明理由，当运动时间t为何值时，点D′恰好落在x轴上？
（3）在平面内，是否存在点P（异于A点），使得以P、B、D为顶点的三角形与△ABD相似（全等除外）？若存在，请直接写出点P的坐标，若不存在，请说明理由．
【答案】（1）抛物线的解析式为y=﹣x2+2x+3，点D的坐标为（1，2）．（2）四边形DMD′N是正方形，理由见解析,经过
s时，点D恰好落在x轴上的D′处．（3）存在，点P的坐标为（1，0）或（2，3）．
【解析】试题分析：（1）先利用待定系数法求得抛物线和直线的解析式，从而得出对称轴与直线的交点；
（2）由抛物线解析式求得点A、B坐标，结合点D坐标可知△ABD为等腰直角三角形，即∠DAB=∠DBA=45°、∠ADB=90°，由翻折性质得D′M=DM、DN=ND′，从而得出四边形MDND′为菱形，根据∠MDN=90°即可得四边形MDND′为正方形；设DM=DN=t，在Rt△D′NB中D′N=t、BN=2
-t、BD′=2，根据勾股定理即可得出t的值；
（3）由△ABD为等腰直角三角形及△PBD与△ABD相似且不全等，知△PBD是以BD为斜边的等腰直角三角形，结合图形即可得答案．
解：（1）将点A（﹣1，0）、C（2，3）代入y=﹣x2+bx+c，
得： 
，解得： 
，
∴抛物线的解析式为y=﹣x2+2x+3，
∵y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴抛物线的对称轴为直线x=1，
设直线AC的函数解析式为y=kx+b，
将A（﹣1，0）、C（2，3）代入y=kx+b，
得： 
，解得： 
，
∴直线AC的函数解析式为y=x+1，
又∵点D是直线AC与抛物线的对称轴的交点，
∴xD=1，yD=1+1=2，
∴点D的坐标为（1，2）．
（2）四边形DMD′N是正方形，理由如下：
∵抛物线y=﹣x2+2x+3与x轴交于A、B两点，
∴令y=0，得﹣x2+2x+3=0，
解得：x1=﹣1，x2=3，
∴A（﹣1，0）、B（3，0），
∴AD=
=2
，BD=
=2
，AB=1+3=4，
而AD2+BD2=AB2，
∴△ABD是等腰直角三角形，
∴∠DAB=∠DBA=45°，∠ADB=90°，
由翻折可知：D′M=DM、DN=ND′，
又∵DM=DN，
∴四边形MDND′为菱形，
∵∠MDN=90°，
∴四边形MDND′是正方形；
设DM=DN=t，当点D落在x轴上的点D′处时，
∵四边形MDND′为正方形，
∴∠D′NB=90°，
在Rt△D′NB中，D′N=t，BN=2
﹣t，BD′=2，
∴t2+（2
﹣t）2=22，
∴t1=t2=
，
即：经过
s时，点D恰好落在x轴上的D′处．
（3）存在，
如图，
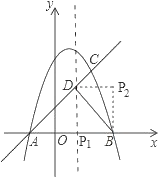
由（2）知△ABD为等腰直角三角形，
∵△PBD与△ABD相似，且不全等，
∴△PBD是以BD为斜边的等腰直角三角形，
∴点P的坐标为（1，0）或（2，3）．
