题目内容
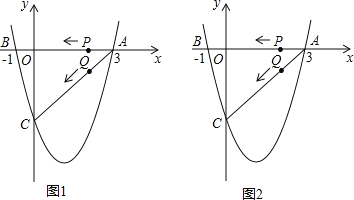
【题目】如图,已知直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]()
与x轴交于A、B两点(A在B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点M是上述抛物线上一点,如果△ABM和△ABC相似,求点M的坐标;
(3)连接AC,求顶点D、E、F、G在△ABC各边上的矩形DEFC面积最大时,写出该矩形在AB边上的顶点的坐标.
【答案】(1)![]() ;(2)M(3,-2);(3)D(
;(2)M(3,-2);(3)D(![]() ,0)或D(-
,0)或D(-![]() ,0)、E(2,0)
,0)、E(2,0)
【解析】试题分析:(1)先求得直线![]() 与x轴交于点B与y轴交于点C的坐标,再把点B的坐标代入
与x轴交于点B与y轴交于点C的坐标,再把点B的坐标代入![]() ,求得b值,即可得抛物线的解析式;(2)先判定△ABC为直角三角形,当△ABM和△ABC相似时,一定有∠AMB=90° ,△BAM≌△ABC,即可得点M的坐标;(3)分矩形DEFG有两个顶点D、E在AB上和矩形一个顶点在AB上两种情况求点的坐标.
,求得b值,即可得抛物线的解析式;(2)先判定△ABC为直角三角形,当△ABM和△ABC相似时,一定有∠AMB=90° ,△BAM≌△ABC,即可得点M的坐标;(3)分矩形DEFG有两个顶点D、E在AB上和矩形一个顶点在AB上两种情况求点的坐标.
试题解析:
(1) 由题意:直线![]() 与x轴交于点B(4,0),
与x轴交于点B(4,0),
与y轴交于点C点C(0,-2),
将点B(4,0)代入抛物线![]() 易得
易得![]()
∴所求抛物线解析式为:![]()
(2) ∵![]() , ∴△ABC为直角三角形,∠BCA=90°
, ∴△ABC为直角三角形,∠BCA=90°
∵点M是上述抛物线上一点∴不可能有MB与AB或者MA与AB垂直
当△ABM和△ABC相似时,一定有∠AMB=90° △BAM≌△ABC
此时点M的坐标为:M(3,-2)
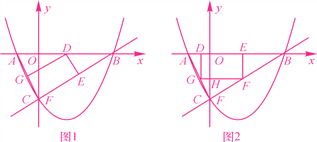
(3)∵△ABC为直角三角形,
∠BCA=90°
当矩形DEFG只有顶点D
在AB上时,显然点F与点
C重合时面积最大,如图1,
设CG=x,
∵DG∥BC,∴△AGD∽△ACB.
∴AG:AC=DG∶BC,即![]() ∴DG=2(
∴DG=2(![]() -x)
-x)
∴S矩形DEFG=-2(x-![]() )
)![]() +
+![]() 即x=
即x=![]() 时矩形DEFG的面积有最大值
时矩形DEFG的面积有最大值![]() (2-x).
(2-x).
∴S矩形DEFG=x·![]() (2-x)=-
(2-x)=-![]() (x-1)2+
(x-1)2+![]() ,即当x=1时矩形DEFG的面积同样有最大值
,即当x=1时矩形DEFG的面积同样有最大值![]() ,
,
综上所述,无论矩形DEFG有两个顶点或只有一个顶点在AB上,其最大面积相同
当矩形一个顶点在AB上时, GD=2(![]() -x)=
-x)=![]() ,AG=
,AG=![]() ,
,
∴AD=![]() , OD=AD-OA=
, OD=AD-OA=![]() , ∴D(
, ∴D(![]() ,0).
,0).
当矩形DEFG有两个顶点D、E在AB上时,∵DG=1, ∴DE=![]() ,
,
∵DG∥OC,∴△ADG∽△AOC,∴AD∶AO=DG∶OC,解得AD=![]() ,
,
∴OD=![]() , OE=
, OE=![]() -
-![]() =2, ∴D(-
=2, ∴D(-![]() ,0),E(2,0).
,0),E(2,0).
综上所述,满足题意的矩形在AB边上的顶点的坐标为D(![]() ,0)或D(-
,0)或D(-![]() ,0)、E(2,0) .
,0)、E(2,0) .

 阅读快车系列答案
阅读快车系列答案