题目内容
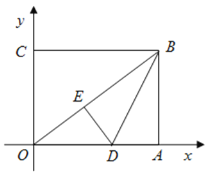
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题.
解:(1)由题知:![]() .
.
(2)设![]() ,则
,则![]() ,
,
根据轴对称的性质,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得 ![]() ,
,
∴![]() ,
,
∴点![]() ,
,
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
则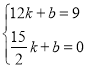 , 解得
, 解得![]() ,
,
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
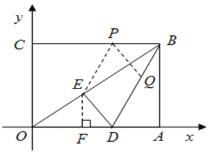
(3)存在,过点![]() 作EP∥DB交
作EP∥DB交![]() 于点
于点![]() ,过点
,过点![]() 作PQ∥ED交
作PQ∥ED交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形.再过点
是平行四边形.再过点![]() 作
作![]() 于点
于点![]() ,
,
由![]() ,
,
得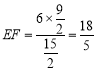 ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() , 解得
, 解得 ![]() , ∴
, ∴![]()
由于EP∥DB,所以可设直线![]() :
:![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() , 解得
, 解得 ![]() ,
,
∴直线![]() :
:![]() ,
,
令![]() ,则
,则![]() ,
,
解得![]() ,
,
∴![]() .
.

【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?





