题目内容
【题目】某公园要修建一个截面抛物线形的拱门,其最大高度为4.5m,宽度OP为6米,现以地面(OP所在的直线)为x轴建立平面直角坐标系(如图1所示)
(1)求这条抛物线的函数表达式;
(2)如图所示,公园想在抛物线拱门距地面3米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?
(3)为修建该拱门,施工队需搭建一个矩形“支架“ABCD(由四根木杆AB﹣BC﹣CD﹣DA组成),使B,C两点在抛物线上.A,D两点在地面OP上(如图2所示),请你帮施工队计算一下最多需要准备多少米该种木杆?
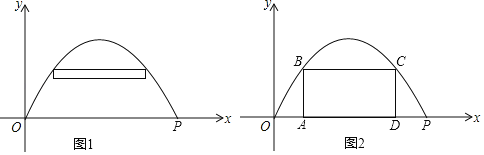
【答案】(1)![]() (2)2
(2)2![]() (3)最多需要准备11米该种木杆.
(3)最多需要准备11米该种木杆.
【解析】
(1)把抛物线的解析式设成顶点式,再代入(6,0),求得结果;
(2)令y=3,求出![]() x2+3x=3的解,再求其横坐标之差的绝对值便可;
x2+3x=3的解,再求其横坐标之差的绝对值便可;
(3)设B(x,![]() x2+3x),用x表示矩形ABCD的周长,根据周长关于x的函数解析式求出其最大值便可.
x2+3x),用x表示矩形ABCD的周长,根据周长关于x的函数解析式求出其最大值便可.
解:(1)由题意知抛物线的顶点坐标为(3,4.5),则
设抛物线的解析式为:y=a(x﹣3)2+4.5,
∵抛物线上有一点(6,0),
∴0=9a+4.5,
∴a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() +4.5,
+4.5,
即y=![]() (0≤x≤6);
(0≤x≤6);
(2)当y=3时,![]() =3,
=3,
解得,![]() ,
,![]() ,
,
∴该横幅的宽度为:(3+![]() )﹣(3﹣
)﹣(3﹣![]() )=2
)=2![]() (米),
(米),
答:该横幅的宽度为2![]() 米;
米;
(3)设B(x,y)
∴B(x,![]() )
)
∵四边形ABCD是矩形,
∴AB=DC=![]() ,
,
根据抛物线的轴对称性,可得:OA=DP=x,
∴AD=6﹣2x,即BC=6﹣2x,
∴令L=AB+BD+DC+AD=2(![]() )+2(6﹣2x)=﹣(x﹣1)2+11.
)+2(6﹣2x)=﹣(x﹣1)2+11.
∴当x=1,L最大值为11,
∴AB、BD、DC、AD的长度之和最大值为11米,/span>
答:最多需要准备11米该种木杆.

练习册系列答案
相关题目