题目内容
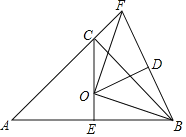
【题目】如图,AB为等腰直角△ABC的斜边(AB为定长线段),E为AB的中点,F为AC延长线上的一个动点,线段FB的垂直平分线交线段CE于点O,D为垂足,当F点运动时,给出下列四个结论,其中一定正确的结论有_____(请填写正确序号)
①O为△ABF的外心;②OF⊥OB;③![]() CE+FC=AB;④FCOB=OEFB
CE+FC=AB;④FCOB=OEFB
【答案】①②④
【解析】
①只要证明OA=OB=OF即可.②利用“8字型”证明∠FCJ=∠JOB=90°即可.③先证明![]() EC+CF=AF,再判断.④正确.证明△OEB∽△FCB即可.
EC+CF=AF,再判断.④正确.证明△OEB∽△FCB即可.
如图,连接AO.

∵CA=CB,AE=EB,
∴CE⊥AB,
∴OA=OB,
∵OD垂直平分线段BF,
∴OF=OB,
∴OA=OF=OB,
∴点O是△ABF的外心,故①正确,
设BC交OF于J.
∵AC=BC,CO=CO,AO=BO,
∴△ACO≌△BCO(SSS),
∴∠CAO=∠CBO,
∵OA=OF,
∴∠CAO=∠CFJ,
∴∠CFJ=∠OBJ,
∵∠CJF=∠OJB,
∴∠JOB=∠JCF=90°,
∴OF⊥OB,故②正确,
∵![]() CE=AC,AC+CF=AF,
CE=AC,AC+CF=AF,
显然AF不一定等于AB,故③错误.
∵∠EBC=∠OBF=45°,
∴∠EBO=∠CBF,
∵∠OEB=∠FCB=90°,
∴△OEB∽△FCB,
∴![]() ∴FCOB=OEFB,故④正确,
∴FCOB=OEFB,故④正确,
故答案为:①②④.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() 是自然数)的函数解析式;
是自然数)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①这100个日需求量所组成的一组数据的中位数和众数分别是________,________;
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进16枝还是17枝?请说明理由.
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.