ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌАыОЖЮЊ1ЕФЁбAЕФдВаФгызјБъдЕуOжиКЯЃЌЯпЖЮBCЕФЖЫЕуЗжБ№дкxжсгыyжсЩЯЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЧвsinЁЯOCB=![]() ЃЎ
ЃЎ
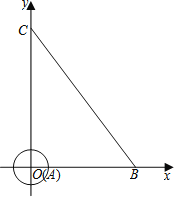
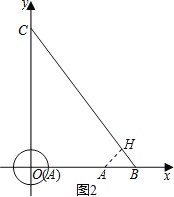
ЃЈ1ЃЉШєЕуQЪЧЯпЖЮBCЩЯвЛЕуЃЌЧвЕуQЕФКсзјБъЮЊmЃЎ
ЂйЧѓЕуQЕФзнзјБъЃЛЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉ
ЂкШєЕуPЪЧЁбAЩЯвЛЖЏЕуЃЌЧѓPQЕФзюаЁжЕЃЛ
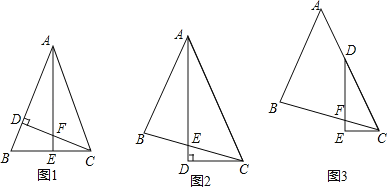
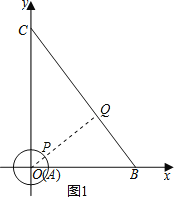
ЃЈ2ЃЉШєЕуAДгдЕуOГіЗЂЃЌвд1ИіЕЅЮЛ/УыЕФЫйЖШбиелЯпOBCдЫЖЏЃЌЕНЕуCдЫЖЏЭЃжЙЃЌЁбAЫцзХЕуAЕФдЫЖЏЖјвЦЖЏЃЎ
ЂйЕуAДгOЁњBЕФдЫЖЏЕФЙ§ГЬжаЃЌШєЁбAгыжБЯпBCЯрЧаЃЌЧѓtЕФжЕЃЛ
ЂкдкЁбAећИідЫЖЏЙ§ГЬжаЃЌЕБЁбAгыЯпЖЮBCгаСНИіЙЋЙВЕуЪБЃЌжБНгаДГіtТњзуЕФЬѕМўЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЉ![]() m+8ЃЛЂкPQзюаЁ=OQзюаЁЉ1=3.8ЃЛЃЈ2ЃЉЂйt=
m+8ЃЛЂкPQзюаЁ=OQзюаЁЉ1=3.8ЃЛЃЈ2ЃЉЂйt=![]() ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЛЂк
ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЛЂк![]() ЃМtЁм5Лђ7ЁмtЁм15ЪБЃЌЁбAгыЯпЖЮBCгаСНИіЙЋЙВЕуЃЎ
ЃМtЁм5Лђ7ЁмtЁм15ЪБЃЌЁбAгыЯпЖЮBCгаСНИіЙЋЙВЕуЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОне§ЧаЕФИХФюЧѓГіBC=10ЃЌOC=8ЃЌдЫгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBCЕФНтЮіЪНЃЌИљОнКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїНтЕУМДПЩЃЛ
ЂкзїOQЁЭABНЛЁбAгкPЃЌдђДЫЪБPQзюаЁЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЂйИљОнЧаЯпЕФаджЪКЭЯрЫЦШ§НЧаЮЕФаджЪМЦЫуМДПЩЃЛ
ЂкНсКЯЭМаЮЁЂдЫгУжБЯпгыдВЕФЮЛжУЙиЯЕЖЈРэНтД№ЃЎ
НтЃКЃЈ1ЃЉЂйЁпЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌtanЁЯOCB=![]() ЃЌ
ЃЌ
ЁрBC=10ЃЌOC=8ЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+bЃЌ
![]() ЃЌ
ЃЌ
НтЕУ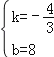 ЃЌ
ЃЌ
ЁпЕуQЕФКсзјБъЮЊmЃЌ
ЁрЕуQЕФзнзјБъЮЊЉ![]() m+8ЃЛ
m+8ЃЛ
ЂкШчЭМ1ЃЌзїOQЁЭABНЛЁбAгкPЃЌдђДЫЪБPQзюаЁЃЌ
![]() ЁСABЁСOQ=
ЁСABЁСOQ=![]() ЁСBOЁСCOЃЌ
ЁСBOЁСCOЃЌ
НтЕУЃЌOQ=4.8ЃЌ
ЁрPQзюаЁ=OQзюаЁЉ1=3.8ЃЛ
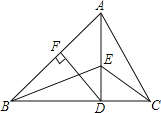
ЃЈ2ЃЉЂйШчЭМ2ЃЌЁбAгыжБЯпBCЯрЧагкHЃЌ
дђAHЁЭBCЃЌгжЁЯBOC=90ЁуЃЌ
ЁрЁїBHAЁзЁїBOCЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃЌBA=![]() ЃЌ
ЃЌ
дђOA=6Љ![]() =
=![]() ЃЌ
ЃЌ
Ёрt=![]() ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЛ
ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЛ
ЂкгЩЃЈ2ЃЉЂйЕУЃЌt=![]() ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЌ
ЪБЃЌЁбAгыжБЯпBCЯрЧаЃЌ
ЕБt=5ЪБЃЌЁбAОЙ§ЕуBЃЌ
ЕБt=7ЪБЃЌЁбAОЙ§ЕуBЃЌ
ЕБt=15ЪБЃЌЁбAОЙ§ЕуCЃЌ
ЙЪ![]() ЃМtЁм5Лђ7ЁмtЁм15ЪБЃЌЁбAгыЯпЖЮBCгаСНИіЙЋЙВЕуЃЎ
ЃМtЁм5Лђ7ЁмtЁм15ЪБЃЌЁбAгыЯпЖЮBCгаСНИіЙЋЙВЕуЃЎ

ЁОЬтФПЁПЮвЪаФГВннЎжжжВХЉЛЇЯВЛёЗсЪеЃЌЙВЪеЛёВннЎ2000kgЃЎОЪаГЁЕїВщЃЌПЩВЩгУХњЗЂЁЂСуЪлСНжжЯњЪлЗНЪНЃЌетСНжжЯњЪлЗНЪНУПkgВннЎЕФРћШѓШчЯТБэЃК
ЯњЪлЗНЪН | ХњЗЂ | СуЪл |
РћШѓЃЈдЊ/kgЃЉ | 6 | 12 |
ЩшАДМЦЛЎШЋВПЪлГіКѓЕФзмРћШѓЮЊyдЊЃЌЦфжаХњЗЂСПЮЊxkgЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєСуЪлСПВЛГЌЙ§ХњЗЂСПЕФ4БЖЃЌЧѓИУХЉЛЇАДМЦЛЎШЋВПЪлЭъКѓЛёЕУЕФзюДѓРћШѓЃЎ