题目内容
【题目】情境观察:
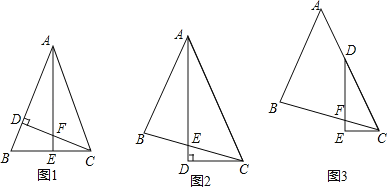
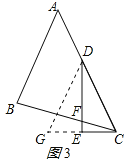
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
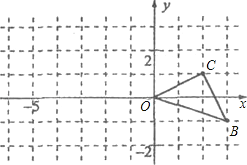
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
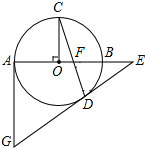
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
【答案】①△ABE≌△ACE,△ADF≌△CDB;②AF=2CE.见解析
【解析】
试题分析:情境观察:①由全等三角形的判定方法容易得出结果;
②由全等三角形的性质即可得出结论;
问题探究:延长AB、CD交于点G,由ASA证明△ADC≌△ADG,得出对应边相等CD=GD,即CG=2CD,证出∠BAE=∠BCG,由ASA证明△ADC≌△CBG,得出AE=CG=2CD即可.
拓展延伸:作DG⊥BC交CE的延长线于G,同上证明三角形全等,得出DF=CG即可.
情境观察:
解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;
故答案为:△ABE≌△ACE,△ADF≌△CDB
②线段AF与线段CE的数量关系是:AF=2CE;
故答案为:AF=2CE.
问题探究:
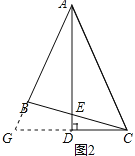
证明:延长AB、CD交于点G,如图2所示:
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
 ,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
 ,
,
∴△ADC≌△CBG中(ASA),
∴AE=CG=2CD.
拓展延伸:
解:作DG⊥BC交CE的延长线于G,
如图3所示.