题目内容
已知：如图在△ABC中，∠C=90°，AD平分∠BAC，交BC于D，若BC=32，且BD：CD=9：7，求：D到AB边的距离．
分析：根据角平分线的性质可得D到AB边的距离=CD，根据BC=32，且BD：CD=9：7，求得CD即可．
解答：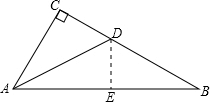
解：过点D作DE⊥AB，则DE是点D到AB的距离
∵BD：CD=9：7，
∴CD=BC•
=32×
=14，
∵AD平分∠CAB，
∴DE=CD=14．
解：过点D作DE⊥AB，则DE是点D到AB的距离∵BD：CD=9：7，
∴CD=BC•
| 7 |
| 16 |
| 7 |
| 16 |
∵AD平分∠CAB，
∴DE=CD=14．
点评：此题主要考查角平分线的性质：角的平分线上的点到角的两边的距离相等．
练习册系列答案
相关题目
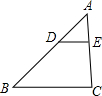已知：如图在△ABC中，DE∥BC，| AD |
| DB |
| 1 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
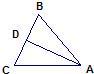9、已知：如图在△ABC中，AD平分∠BAC，AD⊥BC，则△ACD≌△ABD的根据是
已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，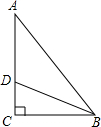
已知：如图在△ABC中，∠C=90°，BD是∠ABC的内角平分线，
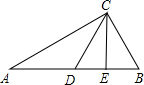已知，如图在△ABC中，∠ACB=90°，AC=8，BC=6，CD、CE分别是斜边AB上的中线和高．则下列结论错误的是（ ）