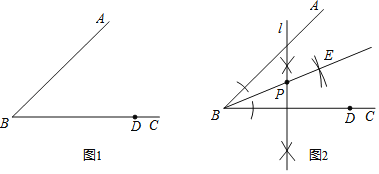��Ŀ����
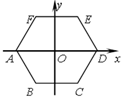
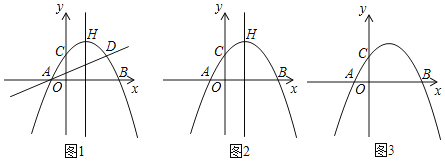
����Ŀ����ͼ����֪ƽ��ֱ������ϵ�У���C��3��4������OCΪ��������OABC���ҵ�A����x����������ϣ���DΪy���ϵ�һ�����㣬��D��0��m��������DB����ֱ��OC�ڵ�E��
��1����գ�B������Ϊ���� ������sin��AOC���� ����
��2������D��y��������ʱ���ǡ�DEO�����ΪS1����BCE�����ΪS2����S1��S2ʱ����m��ֵ��
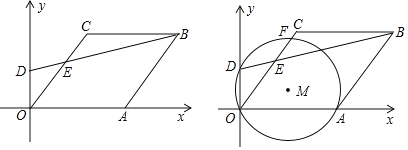
��3������D��O��A����M�����߶�OC�ڵ�F��
������M������OABCһ�����ڵ�ֱ������ʱ������������������m��ֵ��
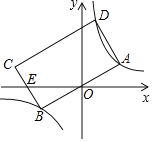
����OD��DEʱ��ֱ��д��OE:EF��ֵ��
���𰸡���1����8��4����![]() ����2��m��
����2��m��![]() ����3��������������m��ֵΪ
����3��������������m��ֵΪ![]() ��
��![]() ����OE:EF��ֵ8:5��
����OE:EF��ֵ8:5��
��������
��1����ͼ1�У���CH��OA��H�����ݵ�C���������OH��CH ���ù��ɶ������OC���ɽ�����⣻
��2����ͼ1�У��ӳ�BC��OD��F����S1=S2���Ƴ�S��OCF=S��BDF���ɴ˹������̼��ɽ�����⣻
��3���ٷ��������Σ���ͼ2�У�����M��BC����ʱ������PQ=DM���������̼��ɽ�����⣮��ͼ3�У�����M��AB����ʱ��AD��AB����AD��OC��Q������tam��OAD=tan��DOC=![]() ���������̼��ɽ�����⣻
���������̼��ɽ�����⣻
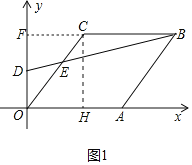
����ͼ4�У���BG��BC��OC���ӳ�����G������DF��AF����FP��OA��P���������BG����֤��BE=BG������DE+BE=BD�������������m����OF=5k����FP=4k��OP=3k����Rt��APF�У�����AF2=PF2+PA2�������������k���ɽ�����⣮
��1����ͼ1�У���CH��OA��H��
��C(3��4)��CH��OA��
��OH��3��CH��4��
��OC��![]() ��
��![]() ��5��
��5��
���ı���ABCD�����Σ�
��OA��AB��OC��BC��5��BC��OA��
��B(8��4)��
��sin��AOC��![]() ��
��![]() ��
��
��2����ͼ1�У��ӳ�BC��OD��F��
��S1��S2��
��S��OCF��S��BDF��
��![]() ��3��4��
��3��4��![]() ��(4��m)��8��
��(4��m)��8��
���m��![]() ��
��
��3������ͼ2�У��ӳ�BC��OD��P����MQ��OD��Q��
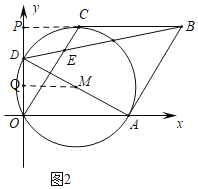
����M��BC����ʱ��PQ��DM��
����4��![]() ��
��![]()
![]() ��
��
���m��![]() ��
��
��ͼ3�У�����M��AB����ʱ��AD��AB����AD��OC��Q��
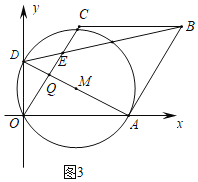
��OC//AB��
��OC��AD��
���AQD��90����
���DOQ+��AOQ��90������AOQ+��OAQ��90����
���DOQ����OAQ��
��tam��OAD��tan��DOC��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��m��![]() ��
��
��������������������m��ֵΪ![]() ��
��![]() ��
��
����ͼ4�У���BG��BC��OC���ӳ�����G������DF��AF����BH��OG��H����FP��OA��P��
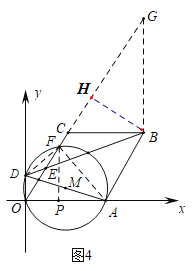
��BC//OA��
��tan��GCB��tan��COA��![]() ��
��![]() ��
��
��BG��![]() ��
��
��OD//BG��
���G����DOE��
��DO��ED��
���DOE����DEO����BEG��
���G����BEG��
��BE��BG��![]() ��
��
��DE+BE��BD��
��(m+![]() )2��82+(4��m)2��
)2��82+(4��m)2��
���m��![]() ��
��
��OF��5k����FP��4k��OP��3k��
�ߡ�ODF����DAF��
��tan��DAF��![]() ��
��![]() ��
��
��sin��DAF��![]() ��
��
��AD��![]() ��
��![]() ��
��
��AF��![]()
![]() ��
��
��Rt��APF����AF2��PF2+PA2��
��![]() ��(m2+25)��(4k)2+(5��3k)2��
��(m2+25)��(4k)2+(5��3k)2��
��m��![]() ���룬�����ã�45k2��54k+13��0��
���룬�����ã�45k2��54k+13��0��
���k��![]() ����ȥ����
����ȥ����![]() ��
��
��OF��![]() ��
��
��sin��G��sin��DAF��![]() ��
��
��GH=![]() ��
��
��EG=2GH=![]() ��
��
��BG//OD��
���ODE�ס�GBE��
��![]() ��
��
��OE��![]() ��
��
��EF��OF��OE��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
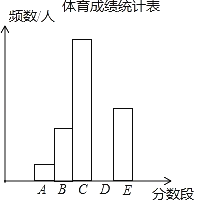
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�����Ŀ��Ϊ���˽�ij�о��꼶ѧ���������ɼ����ɼ���Ϊ�������������ȡ�˲���ѧ���������ɼ����ֶΣ�A��20.5��22.5��B��22.5��24.5��C��24.5��26.5��D��26.5��28.5��E��28.5��30.5��ͳ�ƣ��õ�ͳ��ͼ������ͼ��
������ | A | B | C | D | E | �ϼ� |
Ƶ��/�� | 12 | 36 | 84 | b | 48 | c |
Ƶ�� | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
�����������Ϣ���ش��������⣺
��1��ͳ�Ʊ��У�a���� ����b���� ����c���� ������Ƶ���ֲ�ֱ��ͼ����������
��2��С��˵�����������ݵ�����һ����C�У�������ΪС����˵����ȷ���� ����ѡ���ȷ��������
��3�����ɼ���27�ּ����϶�Ϊ���㣬�����30000�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж��٣�