Question

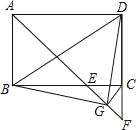
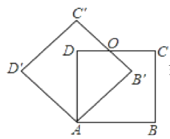
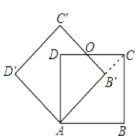
【题目】如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是___.

Answer 1

【答案】4.

【解析】

由边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′，利用勾股定理的知识求出B′C的长，再根据等腰直角三角形的性质，勾股定理可求B′O，OD，从而可求四边形AB′OD的周长．

连接B′C，

∵旋转角∠BAB′=45,∠BAC=45，

∴B′在对角线AC上，

∵AB=AB′=2，

在Rt△ABC中,AC= =2，

∴B′C=2 2，

在等腰Rt△OB′C中,OB′=B′C=22，

在直角三角形OB′C中,OC= (22)=42，

∴OD=2OC=22，

∴四边形AB′OD的周长是：2AD+OB′+OD=4+22+22=4，

故答案为4.