题目内容
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点B的坐标是(0,4),点D的坐标是(8![]() ,4),点M和点N是两个动点,其中点M从点B出发,沿BA以每秒2个单位长度的速度做匀速运动,到点A后停止,同时点N从点B出发,沿折线BC→CD以每秒4个单位长度的速度做匀速运动,如果其中一个点停止运动,则另一点也停止运动,设M,N两点的运动时间为x,△BMN的面积为y,下列图象中能表示y与x的函数关系的图象大致是( )
,4),点M和点N是两个动点,其中点M从点B出发,沿BA以每秒2个单位长度的速度做匀速运动,到点A后停止,同时点N从点B出发,沿折线BC→CD以每秒4个单位长度的速度做匀速运动,如果其中一个点停止运动,则另一点也停止运动,设M,N两点的运动时间为x,△BMN的面积为y,下列图象中能表示y与x的函数关系的图象大致是( )

A.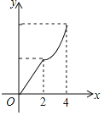 B.
B.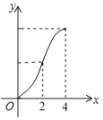 C.
C.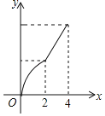 D.
D.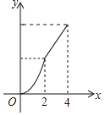
【答案】D
【解析】
根据两个点的运动变化,写出点N在BC上运动时△BMN的面积,再写出当点N在CD上运动时△BMN的面积,即可得出本题的答案;
解:当0<x2时,如图1:
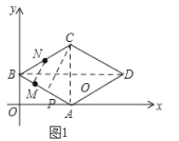
连接BD,AC,交于点O′,连接NM,过点C作CP⊥AB垂足为点P,
∴∠CPB=90°,
∵四边形ABCD是菱形,其中点B的坐标是(0,4),点D的坐标是(8![]() ,4),
,4),
∴BO′=4![]() ,CO′=4,
,CO′=4,
∴BC=AB=![]() ,
,
∵AC=8,
∴△ABC是等边三角形,
∴∠ABC=60°,
∴CP=BC×sin60°=8×![]() =4
=4![]() ,BP=4,
,BP=4,
BN=4x,BM=2x,
![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠NBM=∠CBP,
∴△NBM∽△CBP,
∴∠NMB=∠CPB=90°,
∴![]() ;
;
∴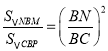 ,
,
即y=![]() ,
,
当2<x4时,作NE⊥AB,垂足为E,
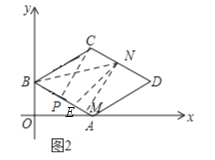
∵四边形ABCD是菱形,
∴AB∥CD,
∴NE=CP=4![]() ,
,
BM=2x,
∴y=![]() ;
;
故选D.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177