题目内容
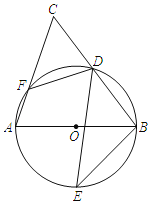
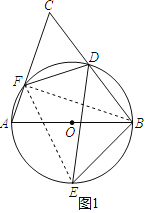
【题目】如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连结BD并延长至点C,使得CD=BD,连结AC交⊙O于点F,连接BE,DE,DF.
(1)若∠E=35°,求∠BDF的度数.
(2)若DF=4,cos∠CFD=![]() ,E是
,E是![]() 的中点,求DE的长.
的中点,求DE的长.
【答案】(1)∠BDF=110°;(2)DE=2![]() +
+![]() .
.
【解析】
(1)连接EF,BF,由AB是⊙O的直径,得到∠AFB=∠BFC=90°,推出![]() ,得到∠DEF=∠BED=35°,根据圆内接四边形的性质即可得到结论;
,得到∠DEF=∠BED=35°,根据圆内接四边形的性质即可得到结论;
(2)连接AD,OE,过B作BG⊥DE于G,解直角三角形得到AB=6,由E是![]() 的中点,AB是⊙O的直径,得到∠AOE=90°,根据勾股定理即可得到结论.
的中点,AB是⊙O的直径,得到∠AOE=90°,根据勾股定理即可得到结论.
(1)如图1,连接EF,BF,
∵AB是⊙O的直径,
∴∠AFB=∠BFC=90°,
∵CD=BD,
∴DF=BD=CD,
∴![]() ,
,
∴∠DEF=∠BED=35°,
∴∠BEF=70°,
∴∠BDF=180°﹣∠BEF=110°;
(2)如图2,连接AD,OE,过B作BG⊥DE于G,

∵∠CFD=∠ABD,
∴cos∠ABD=cos∠CFD=![]() ,
,
在Rt△ABD中,BD=DF=4,
∴AB=6,
∵E是![]() 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵BO=OE=3,
∴BE=3![]() ,
,
∴∠BDE=∠ADE=45°,
∴DG=BG=![]() BD=2
BD=2![]() ,
,
∴GE=![]() =
=![]() ,
,
∴DE=DG+GE=2![]() +
+![]() .
.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
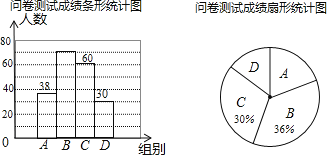
一课一练课时达标系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.
【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.