题目内容
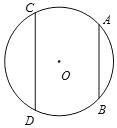
【题目】如图,直径为 10cm 的⊙O 中,两条弦 AB,CD 分别位于圆心的异侧,AB∥CD,且![]() ,若 AB=8cm,则 CD 的长为_____cm.
,若 AB=8cm,则 CD 的长为_____cm.
【答案】![]()
【解析】
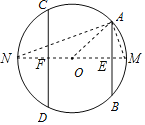
过O作OE⊥AB于E,交⊙O于M,反向延长OE交CD于G,交⊙O于N,则AE=![]() AB=4,连接AN,AO,AM,则MN为⊙O的直径,根据平行线的性质得到MN⊥CD,推出AN=CD,根据勾股定理即可得到结论.
AB=4,连接AN,AO,AM,则MN为⊙O的直径,根据平行线的性质得到MN⊥CD,推出AN=CD,根据勾股定理即可得到结论.
过O作OE⊥AB于E,交⊙O于M,反向延长OE交CD于G,交⊙O于N,
则AE=![]() AB=4,
AB=4,
连接AN,AO,AM,
则MN为⊙O的直径,
∵AB∥CD,
∴MN⊥CD,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AN=CD,
在Rt△AOE中,OE=![]() =3,
=3,
∴ME=5-3=2,
在Rt△AEM中,AM=![]() =2
=2![]() ,
,
∵MN为⊙O的直径,
∴∠MAN=90°,
∴AN=![]() ,
,
∴CD=AN=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目