题目内容
【题目】已知在Rt△ABC中,∠ACB=90°,AC=BC,BM⊥CM于M,且CM>BM
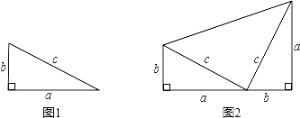
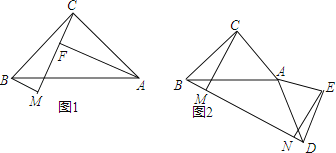
(1)如图1,过点A作AF⊥CM于F,直线写出线段BM、AF、MF的数量关系是
(2)如图2,D为BM延长线上一点,连AD以AD为斜边向右侧作等腰Rt△ADE,再过点E作EN⊥BM于N,求证:CM+EN=MN;
(3)将(2)中的△ADE绕点A顺时针旋转任意角α后,连BD取BD中点P,连CP、EP,作出图形,试判断CP、EP的数量和位置关系并证明.
【答案】(1)AF=BM+MF.(2)证明见解析;(3)CP=PE且CP⊥PE.
【解析】
试题分析:(1)根据全等三角形的判定定理AAS推知△ACF≌△CBM,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换,即可解答;
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,由四边形GMNH为矩形,得到AH⊥EN,根据三垂直得:△CMB≌△AGC,△AEH≌△EDN,利用全等三角形的对应边相等得到相等的线段,即可解答.
(3)取AB的中点M、AD的中点N,连接PM、CM、NE、PN,则可构造△PNE≌CMP,结论不言而喻.
解:(1)AF=BM+MF,
∵∠ACB=90°,
∴∠ACF+∠BCM=90°.
又∵AF⊥CM,
∴∠ACF+∠CAF=90°,
∴∠CAF=∠BCM.
在△ACF和△CBM中,
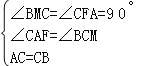 ,
,
∴△ACF≌△CBM,
∴BM=CF,AF=CM,
∴CF+MF=BM+MF=MC=AF,即AF=BM+MF.
故答案为:AF=BM+MF.
(2)如图2,过点A作AG⊥CM于G,反向延长GA交EN于H,
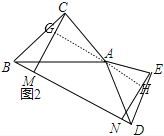
∴四边形GMNH为矩形
∴AH⊥EN
根据三垂直得:△CMB≌△AGC,△AEH≌△EDN,
∴CM=AG,EN=AH,
∴MN=GH=GA+AH=CM+EN.
(3)如图3,
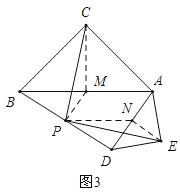
取AB的中点M、AD的中点N,连接PM、CM、NE、PN,
∵△BCA与△AED均为等腰直角三角形,
∴CM=BM=AM,CM⊥BA,
EN=AN=DN,NE⊥AD,
∵P为BD中点,
∴PN=AM=BM=CM,PN∥BA,
PM=AN=DN=NE,PM∥AD,
∴AMPN是平行四边形,
∴∠BMP=∠PND,
∴∠PMC=∠ENP,
∴△PNE≌CMP(SAS),
∴CP=PE,
∵CM⊥AB,PN∥AB,
∴CM⊥PN,
∴CP⊥PE,
综上所述,CP=PE且CP⊥PE.

 小学课时特训系列答案
小学课时特训系列答案