Question

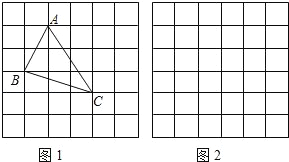
【题目】如图，在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°．

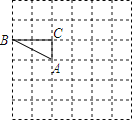
（1）画出旋转后的△AB′C′；

（2）以点C为坐标原点，线段BC、AC所在直线分别为x轴，y轴建立直角坐标系，请直接写出点B′的坐标 ；

（3）写出△ABC在旋转过程中覆盖的面积 ．

Answer 1

【答案】（1）画图见解析；（2）（1，1），（3）π+1．

【解析】

试题分析：（1）利用网格特点和旋转的性质画出点B和C的对应点B′、C′，即可得到△AB′C′；

（2）建立直角坐标系，然后写出点B′的坐标；

（3）根据扇形面积公式，计算S扇形BAB′+S△B′AC′，即可得到△ABC在旋转过程中覆盖的面积．

解：（1）如图，△AB′C′为所作；

（2）如图，点B′的坐标为（1，1）；

（3）△ABC在旋转过程中覆盖的面积=S扇形BAB′+S△B′AC′=+×1×2=π+1．

故答案为（1，1），π+1．