��Ŀ����
�������龳��
������ȤС��ʱ����ʦ������������⣺
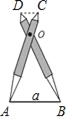
��ͼ�٣���ABC�У���AB��10��AC��8����BC���ϵ�����AD��ȡֵ��Χ.
С�������ھ��������������õ������µĽ���������ӳ�AD����E��ʹDE��AD������BE.�����С���ķ���˼����
(1)����֪����ͼ�ܵõ���ADC�ա�EDB��������( ).
A.SSS B.SAS C.AAS D.HL
(2)�ɡ������ε����߹�ϵ�������AD��ȡֵ��Χ�� .
���˼����Ŀ�г��֡��е㡱�������ߡ����������ɿ����ӳ����߹���ȫ�������Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬһ��������֮��.
���������ã�
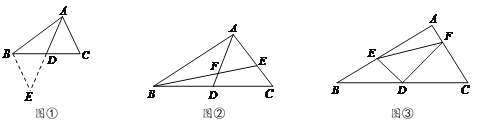
��ͼ�ڣ�AD�ǡ�ABC�����ߣ�BE��AC��E����AD��F����AE��EF.��EF��4��EC��3�����߶�BF�ij�.
��������ã�
��ͼ�ۣ��ڡ�ABC�У���A��90�㣬DΪBC�е㣬 DE��DF��DE��AB�ڵ�E��DF��AC�ڵ�F������EF.�Բ����߶�BE��CF��EF����֮��ĵ�����ϵ����֤����Ľ���.
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ



 ������Ϊ���ֹ��Ʒ����е�����Ϊʲô��
������Ϊ���ֹ��Ʒ����е�����Ϊʲô��
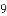
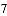
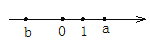
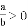
 ��b=
��b= ��
��