Question

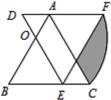
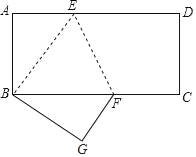
【题目】如图，正方形ABCD的边长AB＝8，E为平面内一动点，且AE＝4，F为CD上一点，CF＝2，连接EF，ED，则2EF+ED的最小值为（　　）

A.12B.12C.12D.10

Answer 1

【答案】B

【解析】

当点E运动到点E′时，在AD边上取AH=2，证明△DAE′∽△E′AH，根据2EF+ED的最小值为2HF的值，再根据勾股定理即可求解．

如图，当点E运动到点E′时，

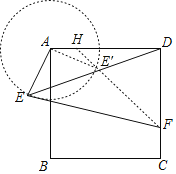
在AD边上取AH＝2，

∵AE′＝AE＝4，

∴AE′：AH＝2：1，

∵AD＝8，

∴AD：AE′＝8：4＝2：1，

∴AD：AE′＝AE′：AH，

∵∠DAE′＝∠E′AH，

∴△DAE′∽△E′AH，

∴DE′：E′H＝2：1，

即DE′＝2E′H，

∵2EF+ED＝2EF+E′D＝2EF+2E′H＝2HF，

∴2EF+ED的最小值即为2HF的值，

∵DH＝AD﹣AH＝6，

DF＝DC﹣CF＝6，

在Rt△DHF中，根据勾股定理，得

HF＝＝6，

∴2HF＝12．

故选：B．