题目内容
【题目】如图,四边形ABCD内接于⊙O.AC为直径,AC、BD交于E,![]() =
=![]() .
.
(1)求证:AD+CD=![]() BD;
BD;
(2)过B作AD的平行线,交AC于F,求证:EA2+CF2=EF2;
(3)在(2)条件下过E,F分别作AB、BC的垂线垂足分别为G、H,连GH、BO交于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O半径.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)延长DA至W,使AW=CD,连接WB,证△BCD和△BAW全等,得到△WBD是等腰直角三角形,然后推出结论;
(2)过B作BE的垂线BN,使BN=BE,连接NC,分别证△AEB和△CNB全等,△BFE和△BFN全等,将EA,CF,EF三条线段转化为直角三角形的三边,即可推出结论;
(3)延长GE,HF交于K,通过大量的面积法的运用,将AE,CF,EF三条线段用含相同的字母表示出来,再根据第二问的结论求出相关字母的值,再求出AB的值,进一步求出⊙O半径.
解:(1)延长DA至W,使AW=CD,连接WB,
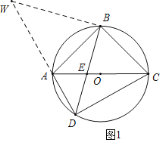
∵![]() =
=![]() ,
,
∴∠ADB=∠CDB=45°,AB=BC,
∵四边形ABCD内接于⊙O.
∴∠BAD+∠BCD=180°,
∵∠BAD+∠WAB=180°,
∴∠BCD=∠WAB,
在△BCD和△BAW中,
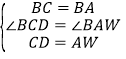 ,
,
∴△BCD≌△BAW(SAS),
∴BW=BD,∠BWA=∠ADB=45°,
∴△WBD是等腰直角三角形,
∴AD+DC=DW=![]() BD;
BD;
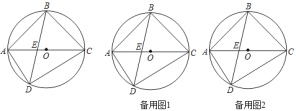
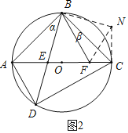
(2)如图2,设∠ABE=α,∠CBF=β,则α+β=45°,
过B作BE的垂线BN,使BN=BE,连接NC,
在△AEB和△CNB中,
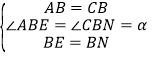 ,
,
∴△AEB≌△CNB(SAS),
∴AE=CN,
∠BCN=∠BAE=45°,
∴∠FCN=90°,
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN,
∴EF=FN,
∵在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
(3)如图3,延长GE,HF交于K,
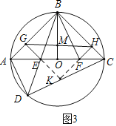
由(2)得EA2+CF2=EF2,
∴![]() EA2+
EA2+![]() CF2=
CF2=![]() EF2,
EF2,
∴S△AGE+S△CFH=S△EFK,
∴S△AGE+S△CFH+S五边形BGEFH=S△EFK+S五边形BGEFH,
即S△ABC=S矩形BGKH,
∴![]() S△ABC=
S△ABC=![]() S矩形BGKH,
S矩形BGKH,
∴S△GBH=S△ABO=S△CBO,
∴S△BGM=S四边形COMH,S△BMH=S四边形AGMO,
∵S四边形AGMO:S四边形COMH=8:9,
∴S△BMH:S△BGM=8:9,
∵BM平分∠GBH,
∴BG:BH=9:8,
设BG=9k,BH=8k,
∴CH=3+k,
∴AE=3![]() ,CF=
,CF=![]() (k+3),EF=
(k+3),EF=![]() (8k-3),
(8k-3),
∴(3![]() )2+[
)2+[![]() (k+3)]2=[
(k+3)]2=[![]() (8k-3)]2,
(8k-3)]2,
整理,得7k2-6k-1=0,
解得:k1=-![]() (舍去),k2=1,
(舍去),k2=1,
∴AB=12,
∴AO=![]() AB=6
AB=6![]() ,
,
∴⊙O半径为6![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案