题目内容
已知:在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的左侧作等腰直角△ADE,解答下列各题:
(1)如果AB=AC,∠BAC=90°.
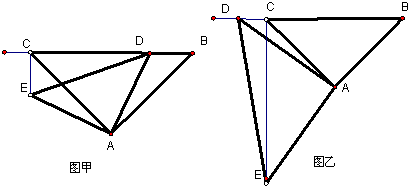
(i)当点D在线段BC上时(与点B不重合),如图甲,线段BD,CE之间的位置关系为
(ii)当点D在线段BC的延长线上时,如图乙,i)中的结论是否还成立?为什么?
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,BC⊥CE(点D不与点C,B重合)?试画出相应图形,写出你的探究结果(不用证明).
(1)如果AB=AC,∠BAC=90°.
(i)当点D在线段BC上时(与点B不重合),如图甲,线段BD,CE之间的位置关系为
BD⊥CE,且BD=CE.
BD⊥CE,且BD=CE.
(ii)当点D在线段BC的延长线上时,如图乙,i)中的结论是否还成立?为什么?

(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,BC⊥CE(点D不与点C,B重合)?试画出相应图形,写出你的探究结果(不用证明).
分析:(1)(i)垂直(或BD⊥CE),相等(或BD=CE);
(ii)(i)中的结论是否仍然成立.由于∠BAC=∠DAE=90°,利用等式性质可得∠BAD=∠CAE,而AB=AC,AD=AE,利用SAS可证△ABD≌△ACE,那么BD=CE,∠B=∠ACE,又知∠B+∠ACB=90°,从而易得∠ACE+∠ACB=∠BCE=90°,即BD⊥CE;
(2)画出和图甲或图乙相似的图即可.
(ii)(i)中的结论是否仍然成立.由于∠BAC=∠DAE=90°,利用等式性质可得∠BAD=∠CAE,而AB=AC,AD=AE,利用SAS可证△ABD≌△ACE,那么BD=CE,∠B=∠ACE,又知∠B+∠ACB=90°,从而易得∠ACE+∠ACB=∠BCE=90°,即BD⊥CE;
(2)画出和图甲或图乙相似的图即可.
解答: 解:(1)(i)垂直(或BD⊥CE),相等(或BD=CE);
解:(1)(i)垂直(或BD⊥CE),相等(或BD=CE);
(ii)(i)中的结论是否仍然成立,理由如下
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE,∠B=∠ACE,
∵∠B+∠ACB=90°,
∴∠ACE+∠ACB=∠BCE=90°,
即BD⊥CE;
(2)如右图所示,
当△ABC满足∠ACB=45°时,BC⊥CE.
 解:(1)(i)垂直(或BD⊥CE),相等(或BD=CE);
解:(1)(i)垂直(或BD⊥CE),相等(或BD=CE);(ii)(i)中的结论是否仍然成立,理由如下
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE,∠B=∠ACE,
∵∠B+∠ACB=90°,
∴∠ACE+∠ACB=∠BCE=90°,
即BD⊥CE;
(2)如右图所示,
当△ABC满足∠ACB=45°时,BC⊥CE.
点评:本题考查了全等三角形的判定和性质.解题的关键是证明△ABD≌△ACE.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.